Optimality Theory
Optimality
Theory ("OT," Prince and Smolensky 1991, 1993) is
a theory of LINGUISTIC UNIVERSALS AND UNIVERSAL GRAMMAR.
According to OT, the grammars of all human languages share a set
of constraints, denoted Con. These constraints are sufficiently
simple and general that they conflict in many contexts: they cannot
all be satisfied simultaneously. The grammar of an individual language
resolves these conflicts: it ranks the universal constraints of Con into a constraint
hierarchy, conflicts being resolved in favor of higher-ranked
constraints, with each constraint having absolute priority over
all lower-ranked constraints. Grammars may differ only in how
they rank the universal constraints; the TYPOLOGY of
all possible human languages may be computed as the result of all
possible rankings of these constraints. An OT analysis explains
why some grammatical patterns are possible while others are not. (That
a particular language happens to have a particular constraint ranking
is not considered a fact to be explained within grammatical theory proper.)
Consider, for example, the difference
between the simple English sentence it rains and its Italian
counterpart piove -- literally, "rains." What
do these sentences reveal about the commonalities and differences between
the two grammars? According to the OT analysis of Grimshaw and Samek-Lodovici
(1995, 1998), at issue here is a conflict between two constraints -- SUBJECT : "Every
sentence has a subject," and FULL-INTERPRETATION : "Every
element of a linguistic expression contributes to its interpretation." In
English, the conflict is resolved in favor of SUBJECT :
to provide a subject, it must appear, even though it has
no referent and contributes nothing to the interpretation of the
sentence, violating FULL-INT . In Italian, the
conflict is resolved the other way: no meaningless subject may appear, and FULL-INT prevails
over SUBJECT .
In many other contexts, SUBJECT and FULL-INT do
not conflict, and both constraints must be satisfied in both languages.
Both constraints are parts of the grammars of both languages, but they
do not have equal status: in English, SUBJECT has
priority, or dominates; we write: SUBJECT >> FULL-INT .
In Italian, the reverse constraint ranking holds. The lower-ranked constraint
in each language must be obeyed, except in contexts in which doing
so would violate the higher-ranked constraint; in this sense, constraints
in OT are minimally violable. OT thus differs from earlier
grammatical theories employing inviolable constraints,
where any violation of a constraint renders a structure ungrammatical
(e.g., RELATIONAL GRAMMAR, LEXICAL FUNCTIONAL GRAMMAR, HEAD-DRIVEN PHRASE STRUCTURE GRAMMAR).
To sketch the broad outline of the
OT picture of cross-linguistic variation, we fix attention on a
universal constraint 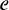 (e.g., FULL-INT). In
some languages,
(e.g., FULL-INT). In
some languages, 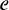 is very highly ranked (e.g., Italian); the effect
is that those linguistic structures (e.g., meaningless it) that
violate the constraint -- those that are marked by
it -- are altogether banned from the language. In other languages,
is very highly ranked (e.g., Italian); the effect
is that those linguistic structures (e.g., meaningless it) that
violate the constraint -- those that are marked by
it -- are altogether banned from the language. In other languages,
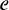 is somewhat lower ranked, so that the structures it marks (e.g., it)
now appear -- but only in those highly restricted contexts
in which the marked element is needed to satisfy one of the few
constraints more highly ranked than
is somewhat lower ranked, so that the structures it marks (e.g., it)
now appear -- but only in those highly restricted contexts
in which the marked element is needed to satisfy one of the few
constraints more highly ranked than 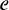 (e.g., SUBJECT in
English). Looking across still other languages,
(e.g., SUBJECT in
English). Looking across still other languages, 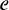 is ranked lower
and lower, so that the structures it marks appear in more and more
contexts, as more and more other constraints force violations of
because they outrank it. The OT literature documents many specific
cases of this general cross-linguistic pattern, which can be captured
entirely by the simple statement:
is ranked lower
and lower, so that the structures it marks appear in more and more
contexts, as more and more other constraints force violations of
because they outrank it. The OT literature documents many specific
cases of this general cross-linguistic pattern, which can be captured
entirely by the simple statement: 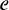
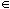 Con. Once
this has been stated, the rest of the pattern follows from the formal
structure of OT: languages differ in how they rank
Con. Once
this has been stated, the rest of the pattern follows from the formal
structure of OT: languages differ in how they rank 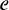 , and depending
on this ranking, those structures marked by
, and depending
on this ranking, those structures marked by 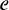 will be either banned altogether
(highest ranking), allowed but only in a highly restricted set of
contexts, or allowed in a wide range of contexts (lowest ranking).
will be either banned altogether
(highest ranking), allowed but only in a highly restricted set of
contexts, or allowed in a wide range of contexts (lowest ranking).
Each universal constraint 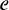 defines
a class of dispreferred or marked structures: those that
violate it. Through the single mechanism of constraint ranking,
such marked elements are banned in some languages, and restricted
in their distribution in all languages. OT thus builds on the notion
of markedness developed in the 1930s by N. S. Trubetzkoy, Roman JAKOBSON,
and others of the Prague Linguistics Circle; OT provides a formal,
general markedness-based calculus within the tradition of GENERATIVE GRAMMAR. OT's formalization of markedness computation
brings into sharp focus a number of issues otherwise obscure.
defines
a class of dispreferred or marked structures: those that
violate it. Through the single mechanism of constraint ranking,
such marked elements are banned in some languages, and restricted
in their distribution in all languages. OT thus builds on the notion
of markedness developed in the 1930s by N. S. Trubetzkoy, Roman JAKOBSON,
and others of the Prague Linguistics Circle; OT provides a formal,
general markedness-based calculus within the tradition of GENERATIVE GRAMMAR. OT's formalization of markedness computation
brings into sharp focus a number of issues otherwise obscure.
Competition
To say that a linguistic
structure S is grammatical in a language L because
it optimally satisfies L's constraint hierarchy
is to exploit a comparative property: even though S might
not satisfy all the universal constraints, every alternative incurs
more serious violations of L's hierarchy than
does S. Specifying an OT grammar includes specifying the candidate
sets of linguistic structures that compete for optimality.
This must be universal, for in OT, only constraint ranking varies
across grammars.
Aggregation of Multiple Dimensions
of Markedness
What defines optimality
when the constraints defining different dimensions of markedness
disagree on which candidate is preferred? OT's answer is
constraint ranking. S is optimal if and only if it is more
harmonic than all other members S" of its
candidate set, written S > S": this means
that, of the constraints differentiating the markedness of S and S",
S is favored by the highest ranked. It is perhaps surprising
that within such a simple mechanism, reranking can succeed in accounting for
such a diversity of observed grammatical patterns.
Faithfulness to Targets
Why is it rains optimal,
when its violation of FULL-INT could be avoided
by selecting another candidate with an interpreted subject, say, John
smiles? Implicit thus far in the competition for optimality
is the target proposition,
<rain(), tense = present>,
to which it rains, but not John smiles, is faithful. In
OT, each candidate is evaluated relative to a target, faithfulness
to which is demanded by constraints in Con collectively
called FAITHFULNESS . John smiles is
indeed optimal, but for a different target,
<smile(x), x = John, tense = present>.
The multiplicity
of grammatical -- optimal -- structures in a single
language arises from the multiplicity of possible targets. In PHONOLOGY,
the target is a sequence of phones, an underlying form such
as /bat + d/ for the past tense of to
bat. Optimal for this target is [bat 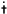 d] "batted";
this includes a vowel ( [
d] "batted";
this includes a vowel ( [ 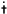 ] )
not present in the target, so it violates a FAITHFULNESS constraint,
] )
not present in the target, so it violates a FAITHFULNESS constraint,
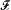 . This minimally unfaithful candidate is optimal because of a universal
constraint against certain word-final consonant clusters, including td; this
constraint is higher ranked than
. This minimally unfaithful candidate is optimal because of a universal
constraint against certain word-final consonant clusters, including td; this
constraint is higher ranked than 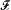 in the phonological component
of the English grammar. That a morpheme (like past-tense /d/)
receives different (but closely related) pronunciations, depending
on its context, follows in OT from a fixed underlying form for the
morpheme, FAITHFULNESS to which is (minimally)
violated in many optimal forms, forced by higher-ranked well-formedness constraints
governing phones in various contexts. Violability of FAITHFULNESS plays
a less obvious role in SYNTAX; Legendre, Smolensky,
and Wilson (1998) use it to explain why some syntactic targets have no grammatical expression
in a particular language: for such an ineffable target, every faithful
candidate violates sufficiently high-ranking constraints that an
unfaithful candidate, with a different interpretation, is optimal.
in the phonological component
of the English grammar. That a morpheme (like past-tense /d/)
receives different (but closely related) pronunciations, depending
on its context, follows in OT from a fixed underlying form for the
morpheme, FAITHFULNESS to which is (minimally)
violated in many optimal forms, forced by higher-ranked well-formedness constraints
governing phones in various contexts. Violability of FAITHFULNESS plays
a less obvious role in SYNTAX; Legendre, Smolensky,
and Wilson (1998) use it to explain why some syntactic targets have no grammatical expression
in a particular language: for such an ineffable target, every faithful
candidate violates sufficiently high-ranking constraints that an
unfaithful candidate, with a different interpretation, is optimal.
The candidates competing for a target I form
a set written Gen(I); I is often called the input, and
sometimes the index, of this candidate set. The set of
targets and the candidate-generating function Gen are universal.
Implications
A framework employing
a novel type of grammatical computation, optimization, OT has cognitive
implications for the classic questions of generative grammar that
concern the nature of knowledge of language, its use, its acquisition,
and its neural realization.
Violable constraints profoundly alter
the analytic options in syntactic theory. When a grammatical sentence S appears to
violate a putative simple, general, universal constraint 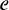 , it becomes
possible to simply say that it actually does; with inviolable
constraints, it is typically necessary to posit invisible structures
that allow S to covertly satisfy
, it becomes
possible to simply say that it actually does; with inviolable
constraints, it is typically necessary to posit invisible structures
that allow S to covertly satisfy 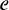 , or to complicate
, or to complicate 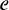 , often
via language-particular parameters, so that it is no longer violated
by S. Topics of OT syntactic analyses include grammatical
voice alternations (GRAMMATICAL RELATIONS and THEMATIC ROLES), case, ANAPHORA, HEAD MOVEMENT, subject
distribution, wh-questions (WH-MOVEMENT),
scrambling, and clitic inventories and placement.
, often
via language-particular parameters, so that it is no longer violated
by S. Topics of OT syntactic analyses include grammatical
voice alternations (GRAMMATICAL RELATIONS and THEMATIC ROLES), case, ANAPHORA, HEAD MOVEMENT, subject
distribution, wh-questions (WH-MOVEMENT),
scrambling, and clitic inventories and placement.
In phonological theory, the shift
from serial, process-oriented frameworks (PHONOLOGICAL RULES AND PROCESSES) to OT's parallel, violable
constraint optimization has enabled explanation of typological variation
in a number of areas: segmental inventories, syllable structure, STRESS, TONE, vowel
harmony, reduplicative and templatic MORPHOLOGY,
phonology-morphology relations, the phonology- PHONETICS interface,
and many others. (For an extensive bibliography and on-line database
of OT papers and software, see the Rutgers Optimality Archive ROA
at http://ruccs.rutgers.edu/roa.html.)
A unified grammatical framework for
syntax and phonology, OT also provides results that span both these
modules, including the relation of general to more specific constraints,
the compatibility among related grammatical processes, and the computation
and learnability of grammars. Formal results on the latter topics
address algorithms for learning constraint rankings from positive
examples, algorithms for computing optimal forms, and the complexity
of formal languages specified by OT grammars. Empirical findings
on the course of acquisition of PHONOLOGY in children,
and on real-time SENTENCE PROCESSING, have
been analyzed within OT. While detailed OT proposals for the neural
basis of language and the neural basis of phonology do not currently
exist, theoretical connections between optimization in OT and in NEURAL NETWORK models have proved fruitful for the continuing
development of both OT and the theory of complex symbol processing
in neural networks (Prince and Smolensky 1997).
See also
Additional links
-- Paul Smolensky
References
Grimshaw, J., and V. Samek-Lodovici. (1995).
Optimal subjects. In J. Beckman, L. Walsh-Dickey, and S. Urbanczyk,
Eds., University of Massachusetts Occasional Papers in Linguistics 18: Papers in
Optimality Theory. Amherst, MA: GLSA, University of Massachusetts,
pp. 589-605.
Grimshaw, J., and V. Samek-Lodovici. (1998).
Optimal subjects and subject universals. In P. Barbosa, D. Fox,
P. Hagstrom, M. McGinnis, and D. Pesetsky, Eds., Is the Best
Good Enough? Papers from the Workshop on Optimality in Syntax. Cambridge,
MA: MIT Press and MIT Working Papers in Linguistics.
Legendre, G., P. Smolensky, and C. Wilson. (1998).
When is less more? Faithfulness and minimal links in wh-chains.
In P. Barbosa, D. Fox, P. Hagstrom, M. McGinnis, and D. Pesetsky,
Eds., Is the Best Good Enough? Papers from the Workshop on
Optimality in Syntax. Cambridge, MA: MIT Press and MIT Working
Papers in Linguistics.
Prince, A., and P. Smolensky. (1991). Notes
on Connectionism and Harmony Theory in Linguistics. Technical
Report CU-CS-533-91. Boulder, CO: Department of Computer Science,
University of Colorado.
Prince, A., and P. Smolensky. (1993). Optimality
Theory: Constraint Interaction in Generative Grammar. RuCCS
Technical Report 2. Piscataway, NJ: Rutgers Center for Cognitive
Science, Rutgers University, and Boulder, CO: Department of Computer
Science, University of Colorado.
Prince, A., and Smolensky, P. (1997). Optimality:
From neural networks to universal grammar. Science 275:1604-1610.
Further Readings
Barbosa, P., D. Fox, P. Hagstrom, M. McGinnis,
and D. Pesetsky, Eds. (1998). Is the Best Good Enough? Papers
from the Workshop on Optimality in Syntax. Cambridge, MA:
MIT Press and MIT Working Papers in Linguistics.
Beckman, J., L. Walsh-Dickey, and S. Urbanczyk,
Eds. (1995). University of Massachusetts Occasional Papers
in Linguistics 18: Papers in Optimality Theory. Amherst,
MA: GLSA, University of Massachusetts.
Grimshaw, J. (1997). Projection, heads, and
optimality. Linguistic Inquiry 28:373-422.
Legendre, G., W. Raymond, and P. Smolensky.
(1993). An Optimality-Theoretic typology of case and grammatical
voice systems. In Proceedings of the Nineteenth Annual Meeting
of the Berkeley Linguistics Society. Berkeley, CA, pp. 464-478.
Legendre, G., and P. Smolensky. (Forthcoming). Towards
a Calculus of the Mind/Brain: Neural Network Theory, Optimality,
and Universal Grammar.
Legendre, G., S. Vikner, and J. Grimshaw, Eds.
(Forthcoming). Optimal Syntax.
McCarthy, J., and A. Prince. (1993). Prosodic
Morphology I: Constraint Interaction and Satisfaction.
RuCCS Technical Report 3. Piscataway, NJ: Rutgers Center for Cognitive
Science, Rutgers University.
McCarthy, J., and A. Prince. (1993). Generalized
Alignment. In G. Booij and J. van Marle, Eds., Yearbook of
Morphology 1993. Dordrecht: Kluwer, pp. 79-153.
McCarthy, J., and A. Prince. (1995). Faithfulness
and reduplicative identity. In J. Beckman, L. Walsh Dickey, and
S. Urbanczyk, Eds., University of Massachusetts Occasional
Papers in Linguistics 18: Papers in Optimality Theory. Amherst, MA:
GLSA, University of Massachusetts, pp. 249-384.
Smolensky, P. (1996). On the comprehension/production
dilemma in child language. Linguistic Inquiry 27:720-731.
Tesar, B., and P. Smolensky. (1998). Learnability
in Optimality Theory. Linguistic Inquiry 29:229-268.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
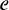 (e.g., FULL-INT). In
some languages,
(e.g., FULL-INT). In
some languages, 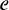 is very highly ranked (e.g., Italian); the effect
is that those linguistic structures (e.g., meaningless it) that
violate the constraint -- those that are marked by
it -- are altogether banned from the language. In other languages,
is very highly ranked (e.g., Italian); the effect
is that those linguistic structures (e.g., meaningless it) that
violate the constraint -- those that are marked by
it -- are altogether banned from the language. In other languages,
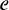 is somewhat lower ranked, so that the structures it marks (e.g., it)
now appear -- but only in those highly restricted contexts
in which the marked element is needed to satisfy one of the few
constraints more highly ranked than
is somewhat lower ranked, so that the structures it marks (e.g., it)
now appear -- but only in those highly restricted contexts
in which the marked element is needed to satisfy one of the few
constraints more highly ranked than 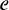 (e.g., SUBJECT in
English). Looking across still other languages,
(e.g., SUBJECT in
English). Looking across still other languages, 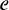 is ranked lower
and lower, so that the structures it marks appear in more and more
contexts, as more and more other constraints force violations of
because they outrank it. The OT literature documents many specific
cases of this general cross-linguistic pattern, which can be captured
entirely by the simple statement:
is ranked lower
and lower, so that the structures it marks appear in more and more
contexts, as more and more other constraints force violations of
because they outrank it. The OT literature documents many specific
cases of this general cross-linguistic pattern, which can be captured
entirely by the simple statement: 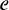
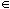 Con. Once
this has been stated, the rest of the pattern follows from the formal
structure of OT: languages differ in how they rank
Con. Once
this has been stated, the rest of the pattern follows from the formal
structure of OT: languages differ in how they rank 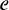 , and depending
on this ranking, those structures marked by
, and depending
on this ranking, those structures marked by 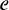 will be either banned altogether
(highest ranking), allowed but only in a highly restricted set of
contexts, or allowed in a wide range of contexts (lowest ranking).
will be either banned altogether
(highest ranking), allowed but only in a highly restricted set of
contexts, or allowed in a wide range of contexts (lowest ranking).
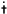 d] "batted";
this includes a vowel ( [
d] "batted";
this includes a vowel ( [ 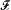 . This minimally unfaithful candidate is optimal because of a universal
constraint against certain word-final consonant clusters, including td; this
constraint is higher ranked than
. This minimally unfaithful candidate is optimal because of a universal
constraint against certain word-final consonant clusters, including td; this
constraint is higher ranked than