Distributed vs. Local Representation

A central problem for cognitive science is to understand how agents represent the information that enables them to behave in sophisticated ways. One long-standing concern is whether representation is localized or distributed (roughly, "spread out"). Two centuries ago Franz Josef Gall claimed that particular kinds of knowledge are stored in specific, discrete brain regions, whereas Pierre Flourens argued that all knowledge is spread across the entire cortex (Flourens 1824; Gall and Spurzheim 1809/1967). This debate has continued in various guises through to the present day (e.g., Farah 1994). Meanwhile, the concept of distribution has found mathematical elaboration in fields such as optics and psychology, and the rise of connectionist models has generated interest in a range of related technical and philosophical issues.

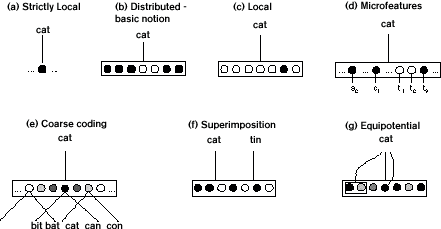
In the most basic sense, a distributed representation is one that is somehow "spread out" over some more-than-minimal extent of the resources available for representing. Unfortunately, however, this area is a semantic mess; the terms local and distributed are used in many different ways, often vaguely or ambiguously. Figure 1 sketches the most common meanings.

Figure 1

Figure 1 Seven ways to represent the word "cat," illustrating varieties of local and distributed representation.

Suppose that we have some quantity of resources available for representing items, and that these resources are naturally divisible into minimal chunks or aspects. Connectionist neural processing units are obvious examples, but the discussion here is pitched at a very abstract level, and the term "unit" in what follows might just as well refer to bits in a digital computer memory, single index cards, synaptic interconnections, etc.

  1. Strictly Local The item (in this case, the word "cat") is represented by appropriately configuring a single dedicated unit. The state of the other units is irrelevant.
  2. Distributed -- basic notion The word is represented by a distinctive configuration pattern over some subset or "pool" of the available resources (see Hinton, McClelland, and Rumelhart 1986). A different word would be represented by an alternative pattern over that pool or another pool. Each unit in the pool participates in representing the word; the state of units outside the pool are irrelevant. In a sparse (dense) distributed representation, a small (large) proportion of units in the pool are configured in a non-default or "active" state (Kanerva 1988).
  3. Local The limiting case of a sparse distributed representation is one in which only a single unit in the pool is active. These representations are often also referred to as "local" (e.g., Thorpe 1995). The key difference with strictly local representations is that here it matters what state the other units in the pool are in, viz., they must not be active.
  4. Microfeatures Sometimes individual units are used to represent "microfeatures" of the domain in strictly local fashion. The pattern representing a given macro-level item is then determined by these microfeatural correspondences. In the example in Figure 1, individual units represent the presence of a letter at a certain spot in the word; the word "cat" is represented just in case the active units are the ones for c in the first spot, a in the second spot, and t in the third spot.
  5. Coarse Coding In these schemes the (micro or macro) features of the domain represented by individual units are relatively broad, and overlapping.

The reader seeking a detailed illustration of these ideas may care to examine the well-known "verb-ending" paper of Rumelhart and McClelland (1986). In that case, verb-base and past-tense forms are represented by sparse distributed patterns over pools of units. Individual units represent microfeatures (ordered triples of phonetic features) in strictly local fashion. Because these triples overlap, the scheme is also coarse.

  1. Superimposition Two or more items are simultaneously represented by one and the same distributed pattern (Murdock 1979). For example, it is standard in feedforward connectionist networks for one and the same set of synaptic weights to represent many associations between input and output.
  2. Equipotentiality In some cases, an item is represented by a pattern over a pool of units, and the pattern over any subpool (up to some resolution limit) also suffices to represent the item. Thus every part or aspect of the item is represented in superimposed fashion over the whole pool. The standard example is the optical hologram (Leith and Uptanieks 1965); see also Plate's "holographic reduced" representations (Plate 1993).

With these various distinctions on board, we can return to the central question: is human knowledge represented in distributed form? This question has been approached at a number of levels, ranging from detailed neurophysiology to pure philosophy of mind. Thus, neuroscientists have debated whether the patterns of neural firing responsible for representing some external event are a matter of single cells (Barlow 1972) or patterns of activity distributed over many cells; if the latter, whether the patterns are sparse, dense, or coarse-coded (e.g., Földiák and Young 1995). At a higher level, they have debated whether knowledge is distributed over large areas of the brain, perhaps in equipotential fashion (LASHLEY 1929/1963), or whether at least some kinds of knowledge are restricted to tightly circumscribed regions (Fodor 1983).

These issues have also been pursued in the context of computer-based cognitive modeling. Connectionists have paid considerable attention to the relative merits of distributed versus local encoding in their networks. Advantages of distribution are generally held to include greater representational capacity, content addressibility, automatic generalization, fault tolerance, and biological plausibility. Disadvantages include slow learning, catastrophic interference (French 1992), and binding problems.

In a famous critique of connectionist cognitive science, Fodor and Pylyshyn (1988) argued that connectionists must either implement "classical" architectures with their traditional symbolic representations or fail to explain the alleged "systematicity" of cognition. The standard connectionist response has been to insist that they can in fact explain systematicity without merely implementing classical architectures by using distributed representations encoding complex structures in a nonconcatenative fashion (e.g., Smolensky 1991).

Implicit in this connectionist response is the idea that distributed representations and standard symbolic representations are somehow deeply different in nature. For millennia, philosophers have attempted to develop a taxonomy of representations. At the highest level, they have usually distinguished just two major kinds -- the generically linguistic or symbolic, and the generically imagistic or pictorial. Is distribution just an accidental property of these more basic kinds, or do distributed representations form a third fundamental category?

Answers to questions like these obviously depend on exactly what we mean by "distributed." The standard approach, as exemplified in the preceding discussion, has been to define various notions of distribution in terms of structures of correspondence between the represented items and the representational resources (e.g., van Gelder 1992). This approach may be misguided; the essence of this alternative category of representation might be some other property entirely. For example, Haugeland (1991) has suggested that whether a representation is distributed or not turns on the nature of the knowledge it encodes.

It has been argued that some of the most intransigent problems confronting orthodox artificial intelligence are rooted in its commitment to representing knowledge by means of digital symbol structures (Dreyfus 1992). If this is right, there must be some other form of knowledge representation underlying human capacities. If distributed representation is indeed a fundamentally different form of representation, it may be suited to playing this role (Haugeland 1978).

See also

Additional links

-- Tim van Gelder

References

Barlow, H. B. (1972). Single units and sensation. Perception 1:371-394.

Dreyfus, H. L. (1992). What Computers Still Can't Do: A Critique of Artificial Reason. Cambridge MA: The MIT Press.

Farah, M. (1994). Neuropsychological inference with an interactive brain. Behavioral and Brain Sciences 17:43-61.

Flourens, P. (1824). Recherches Expérimentales sur les Propriétés et les Fonctions du Systeme Nerveux. Paris: Grevot.

Fodor, J. A. (1983). The Modularity of Mind. Cambridge MA: Bradford/MIT Press.

Fodor, J. A., and Z. Pylyshyn. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition 28:3-71.

Földiák, P., and M. P. Young. (1995). Sparse coding in the primate cortex. In M. A. Arbib, Ed., The Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press, pp. 895-898.

French, R. (1992). Semi-distributed representations and catastrophic forgetting in connectionist networks. Connection Science 4:365-377.

Gall, F. J., and J. G. Spurzheim. (1809/1967). Recherches sur le Systeme Nerveux. Amsterdam: Bonset.

Haugeland, J. (1978). The nature and plausibility of cognitivism. Behavioral and Brain Sciences 1:215-226.

Haugeland, J. (1991). Representational genera. In W. Ramsey, S. P. Stich, and D. E. Rumelhart, Eds., Philosophy and Connectionist Theory. Hillsdale, NJ: Lawrence Erlbaum Associates, pp. 61-89.

Hinton, G. E., J. L. McClelland, and D. E. Rumelhart. (1986). Distributed representations. In D. E. Rumelhart and J. L. McClelland, Eds., Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge, MA: MIT Press, pp. 77-109.

Kanerva, P. (1988). Sparse Distributed Memory. Cambridge, MA: MIT Press.

Lashley, K. S. (1929/1963). Brain Mechanisms and Intelligence: A Quantitative Study of Injuries to the Brain. New York: Dover.

Leith, E. N., and J. Uptanieks. (1965). Photography by laser. Scientific American 212(6):24-35.

Murdock, B. B. (1979). Convolution and correlation in perception and memory. In L. G. Nilsson, Ed., Perspectives on Memory Research, pp. 609-626. Hillsdale, NJ: Lawrence Erlbaum Associates.

Plate, T. A. (1993). Holographic recurrent networks. In C. L. Giles, S. J. Hanson, and J. D. Cowan, Eds., Advances in Neural Processing Systems 5 (NIPS92). San Mateo, CA: Morgan Kaufmann.

Rumelhart, D. E., and J. L. McClelland. (1986). On learning the past tenses of English verbs. In J. L. McClelland, D. E. Rumelhart, and The PDP Research Group, Eds., Parallel Distributed Processing: Explorations in the Microstructure of Cognition. vol. 2: Psychological and Biological Models. Cambridge, MA: MIT Press, pp. 216-268.

Smolensky, P. (1991). Connectionism, constituency, and the language of thought. In B. Lower and G. Rey, Eds., Jerry Fodor and his Critics. Oxford: Blackwell.

Thorpe, S. (1995). Localized versus distributed representations. In M. A. Arbib, Ed., Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press, pp. 549-552.

van Gelder, T. J. (1990). Compositionality: A connectionist variation on a classical theme. Cognitive Science 14:355-384.

van Gelder, T. J. (1991). What is the 'D' in 'PDP'? An overview of the concept of distribution. In S. Stich, D. Rumelhart, and W. Ramsey, Eds., Philosophy and Connectionist Theory. Hillsdale, NJ: Lawrence Erlbaum Associates, pp. 33-59.

van Gelder, T. J. (1992). Defining "distributed representation." Connection Science 4:175-191.

MIT Press Copyright © 1999 Massachusetts Institute of Technology