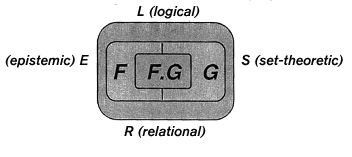
Figure 1Conceptual structure of fuzzy logic.
What is fuzzy logic? This question does not have a simple answer because fuzzy logic, or FL for short, has many distinct facets -- facets that overlap and have unsharp boundaries (Zadeh 1996a; Dubois, Prade, and Yager 1993).
To a first approximation, fuzzy logic is a body of concepts, constructs, and techniques that relate to modes of reasoning that are approximate rather than exact. Much of -- perhaps most -- human reasoning is approximate in nature. In this perspective, the role model for fuzzy logic is the human mind. By contrast, classical LOGIC is normative in spirit in the sense that it is aimed at serving as a role model for human reasoning rather than having the human mind as its role model. Fundamentally, fuzzy logic is a generalization of classical logic and rests on the same mathematical foundations. However, as a generalization that reflects the pervasive imprecision of human reasoning, fuzzy logic is much better suited than classical logic to serve as the logic of human cognition.
Among the many facets of fuzzy logic there are four that stand out in importance. They are the following:

Figure 1Conceptual structure of fuzzy logic.
The logical facet of FL, FL/L , is a logical system or, more accurately, a collection of logical systems that include as a special case both two-valued and multiple-valued systems. As in any logical system, at the core of the logical facet of FL lies a system of rules of inference. In FL/L, however, the rules of inference play the role of rules that govern propagation of various types of fuzzy constraints. Concomitantly, a proposition, p, is viewed as a fuzzy constraint on an explicitly or implicitly defined variable. For example, the proposition "Mary is young" may be viewed as a fuzzy constraint on the variable Age (Mary), with "young" playing the role of a constraining fuzzy relation. Similarly, the proposition "Most students are young" may be viewed as a fuzzy constraint on the proportion of young students among students, with the fuzzy quantifier "most" playing the role of a fuzzy constraint on the proportion. The logical facet of FL plays a pivotal role in the applications of FL to knowledge representation and to inference from information that is imprecise, incomplete, uncertain, or partially true.
The set-theoretic facet of FL, FL/S, is concerned with fuzzy sets, that is, classes or sets whose boundaries are not sharply defined. The initial development of FL was focused on this facet. Most of the applications of FL in mathematics have been and continue to be related to the set-theoretic facet. Among the examples of such applications are: fuzzy topology, fuzzy groups, fuzzy differential equations, and fuzzy arithmetic. Actually, any concept, method or theory can be generalized by fuzzification, that is, by replacing the concept of a set with that of a fuzzy set. Fuzzification serves an important purpose: it provides a way of constructing theories that are more general and more reflective of the imprecision of the real world than theories in which the sets are assumed to be crisp.
The relational facet of FL, FL/R, is concerned in the main with representation and manipulation of imprecisely defined functions and relations. It is this facet of FL that plays a pivotal role in its applications to systems analysis and control. The three basic concepts that lie at the core of this facet of FL are those of a linguistic variable, fuzzy if-then rule, and fuzzy graph. The relational facet of FL provides a foundation for the fuzzy-logic-based methodology of computing with words (CW).
Basically, a linguistic variable is a variable whose values are words drawn from a natural or synthetic language, with words playing the role of labels of fuzzy sets. For example, Height is a linguistic variable if its values are assumed to be: tall, very tall, quite tall, short, not very short, and so on. The concept of a linguistic variable plays a fundamentally important role in fuzzy logic and in particular, in computing with words. The use of words instead of -- or in addition to -- numbers serves two major purposes: (1) exploitation of the tolerance for imprecision; and (2) reflection of the finite ability of the human mind to resolve detail and store precise information.
The epistemic facet of FL, FL/E, is linked to its logical facet and is focused on the applications of FL to knowledge representation, information systems, fuzzy databases, and the theories of possibility and probability. A particularly important application area for the epistemic facet of FL relates to the conception and design of information/intelligent systems.
At the core of FL lie two basic concepts: (1) fuzziness/fuzzification; and (2) granularity/granulation. As was al-luded to already, fuzziness is a condition that relates to classes whose boundaries are not sharply defined, whereas fuzzification refers to replacing a crisp set, that is, a set with sharply defined boundaries, with a set whose boundaries are fuzzy. For example, the number 5 is fuzzified when it is transformed into approximately 5.
In a similar spirit, granularity relates to clumpiness of structure, whereas granulation refers to partitioning an object into a collection of granules, with a granule being a clump of objects (points) drawn together by indistinguishability, similarity, proximity, or functionality. For example, the granules of an article might be the introduction, section 1, section 2, and so forth. Similarly, the granules of a human body might be the head, neck, chest, stomach, legs, and so on. Granulation may be crisp or fuzzy, dense or sparse, physical or mental.
A concept that plays a pivotal role in fuzzy logic is that of fuzzy information granulation, or fuzzy IG, for short. In crisp IG, the granules are crisp, whereas in fuzzy IG the granules are fuzzy. For example, when the variable Age is granulated into the time intervals {0,1}, {1,2}, {2,3}, . . . , the granules {0,1}, {1,2}, {2,3}, . . . are crisp; when Age is treated as a linguistic variable, the fuzzy sets labeled young, middle-aged, old, are fuzzy granules that play the role of linguistic values of Age. The importance of fuzzy logic -- especially in the realm of applications -- derives in large measure from the fact that FL is the only methodology that provides a machinery for fuzzy information granulation. In the figure, the core concept of fuzzy granulation is represented as the conjunction F. G.
The point of departure in fuzzy logic is the concept of a fuzzy set. A fuzzy set A in a universe U is characterized by its grade of membership µA, which associates with every point u in U its grade of membership µA(u), with µA(u) taking values in the unit interval [0,1]. More generally, µA may take values in a partially ordered set. For crisp sets, the concept of a membership function reduces to the familiar concept of a characteristic function, with µA(u) being 1 or 0 depending, respectively, on whether u belongs or does not belong to A.
Two interpretations of A play basic roles in fuzzy logic: possibilistic and veristic. More specifically, assume that X is a variable taking values in U, and A is a fuzzy set in U. In the possibilistic interpretation, in the proposition X is A, A plays the role of the possibility distribution of X, and µ A(u) is the possibility that X can take the value u. In the veristic interpretation, µA(u) is the truth value (verity) of the proposition X = u. As an illustration, in the proposition Mary is young if µyoung(25) = 0.8, then the possibility that Mary is twenty-five given that Mary is young is 0.8. Reciprocally, given that Mary is 25, the truth value (verity) of the proposition Mary is young is 0.8.
In addition to the concept of a fuzzy set, the basic concepts in fuzzy logic are those of a linguistic variable, fuzzy if-then rule, and fuzzy graph. In combination, these concepts provide a foundation for the theory of fuzzy information granulation (Zadeh 1997), the calculus of fuzzy if-then rules (Zadeh 1996a), and, ultimately, the methodology of computing with words (Zadeh 1996b). Most of the practical applications of fuzzy logic, especially in the realm of control and information/intelligent systems, involve the use of the machinery of computing with words.
Fuzzy if-then rules can assume a variety of forms. The simplest rule can be expressed as: if X is A then Y is B, where X and Y are variables taking values in universes of discourse U and V, respectively; and A and B are fuzzy sets in U and V. Generally, A and B play the role of linguistic values of X and Y; for example, if Pressure is high then Volume is low. In practice, the membership functions of A and B are usually triangular or trapezoidal.
A fuzzy graph is a union of fuzzy points (granules) each of which represents a fuzzy if-then rule. A fuzzy graph of a function f may be interpreted as a granular approximation to f. In most of the practical applications of fuzzy logic, fuzzy graphs are employed in this role as granular approximations to functions and relations.
In computing with words, the initial data set (IDS) and the terminal data set (TDS) are assumed to consist of collections of propositions expressed in a natural language. An input interface transforms IDS into a system of fuzzy constraints that are propagated from premises to conclusions through the use of the inference rules in fuzzy logic. The output interface transforms the conclusions into TDS.
The machinery for computing with words instead of or in addition to numbers may be viewed as one of the principal contributions of fuzzy logic. In a way, computing with words may be regarded as a step toward a better understanding of the remarkable human ability to perform complex tasks without any measurements and any numerical computations.
Dubois, D., H. Prade, and R. Yager. (1993). Readings in Fuzzy Sets for Intelligent Systems. San Mateo: Morgan Kaufmann.
Zadeh, L. A. (1996a). Fuzzy Sets, Fuzzy Logic and Fuzzy Systems. Singapore: World Scientific.
Zadeh, L. A. (1996b). Fuzzy logic and the calculi of fuzzy rules and fuzzy graphs: a precis. Multiple Valued Logic 1:1-38.
Zadeh, L. A. (1996c). Fuzzy logic = computing with words. IEEE Transactions on Fuzzy Systems 4(2):103-111.
Zadeh, L. A. (1997). Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets and Systems 90:111-127.