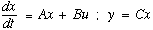
The modern development of automatic control evolved from the regulation of tracking telescopes, steam engine control using fly-ball governors, the regulation of water turbines, and the stabilization of the steering mechanisms of ships. The literature on the subject is extensive, and because feedback control is so broadly applicable, it is scattered over many journals ranging from engineering and physics to economics and biology. The subject has close links to optimization including both deterministic and stochastic formulations. Indeed, Bellman's influential book on dynamic optimization, Dynamic Programming (1957), is couched largely in the language of control.
The successful use of feedback control often depends on having an adequate model of the system to be controlled and suitable mechanisms for influencing the system, although recent work attempts to bypass this requirement by incorporating some form of adaptation, learning, or both. Here we will touch on the issues of modeling, regulation and tracking, optimization, and stochastics.
Modeling
The oldest and still
most successful class of models used to design and analyze control
systems are input-output models, which capture how certain controllable
input variables influence the state of the system and, ultimately,
the observable outputs. The models take the form of differential
or difference equations and can be linear or nonlinear, finite or
infinite dimensional. When possible, the models are derived from
first principles, adapted and simplified to be relevant to the situation
of interest. In other cases, empirical approaches based on regression
or other tools from time series analysis are used to generate a
mathematical model from data. The latter is studied under the name
of "system identification" (Willems 1986). To
fix ideas, consider a linear differential equation model with input
vector u, state vector x, and output y
Equation 1
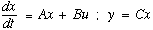
There are important classes of systems whose performance can only be explained by nonlinear models. Many of these are prominent in biology. In particular, problems that involve pattern generation, such as walking or breathing, are not well modeled using linear equations. The description of numerically controlled machine tools and robots, both of which convert a formal language input into an analog (continuous) output are also not well modeled by the linear theory, although linear theory may have a role in explaining the behavior of particular subsystems (Brockett 1997, 1993).
Regulation and Tracking
The simplest and most
frequently studied problem in automatic control is the regulation
problem. Here one has a desired value for a variable, say the level
of water in a tank, and wants to regulate the flow of water into
the tank to keep the level constant in the face of variable demand.
This is a special case of the problem of tracking a desired signal,
for example, keeping a camera focused on a moving target (see STEREO AND MOTION PERCEPTION), or orchestrating the motion of a
robot so that the end effector follows a certain moving object.
The design of stable regulators is one of the oldest problems in
control theory. It is often most effective to incorporate additional
dynamic effects, such as integral action, in the feedback
path, thus increasing the complexity of the dynamics and making
the issue of stability less intuitive. In the case of systems adequately
modeled by linear differential equations, the matter was resolved
long ago by the work of Routh, and Hurwitz, which yields, for example,
the result that the third-order linear, constant-coefficient differential
equation
Equation 2
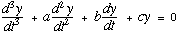
Optimization
A systematic approach
to the design of feedback regulators can be based on the minimization
of the integral of some positive function of the error and the control
effort. For the linear system defined above this might take the
form
Equation 3
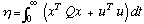
which leads, via the calculus of variations, to a linear feedback control law of the form u = - BTKx, with K being a solution to the quadratic matrix equation AT K + KA - KBB T K + Q = 0. This methodology provides a reasonably systematic approach to the design of regulators in that only the loss matrix Q is unspecified. Different types of optimization problems associated with trajectory optimization in aerospace applications and batch processing in chemical plants are also quite important. A standard problem formulation in this latter setting would be concerned with problems of the form
Equation 4
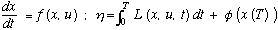
Stochastics
The Kalman- Bucy (1961)
filter, one of the most widely appreciated triumphs of mathematical
engineering, is used in many fields to reduce the effects of measurement
errors and has played a significant role in achieving the first
soft landing on the moon, and more recently, achieving closed-loop
control of driverless cars on the autobahns of Germany. Developed
in the late 1950s as a state space version of the Wiener-Kolomogorov
theory of filtering and prediction, it gave rise to a rebirth of
this subject. In its basic form, the Kalman-Bucy filter is based
on a linear system, white noise (written here as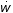 
and 
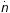) model
Equation 5
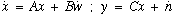
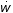by passing it into the linear system,
although it is not observed directly, but only after it is corrupted
by the additive noise 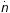. The theory
tells us that the best (in several senses including the least squares)
way to recover x from y is to generate an estimate 
using the equation
Equation 6
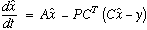
Equation 7
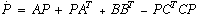
Airy, G. B. (1840). On the regulator of the clock-work for effecting uniform movement of equatoreals. Memoirs of the Royal Astronomical Society 11:249-267.
Bellman, R. (1957). Dynamic Programming. Princeton: Princeton University Press.
Brémaud, P. (1981). Point Processes and Queues. New York: Springer.
Brockett, R. W. (1970). Finite Dimensional Linear Systems. New York: Wiley.
Brockett, R. W. (1993). Hybrid models for motion control systems. In H. Trentelman and J. C. Willems, Eds., Perspectives in Control. Boston: Birkhauser, pp. 29-54.
Brockett, R. W. (1997). Cycles that effect change. In Motion, Control and Geometry. Washington, DC: National Research Council, Board on Mathematical Sciences.
Hurwitz, A. (1895). Über die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt. Mathematische Annalen 46:273-284.
Kalman, R. E., and R. S. Bucy. (1961). New results in linear filtering and prediction theory. Trans. ASME Journal of Basic Engineering 83:95-108.
Kalman, R. E., et al. (1969). Topics in Mathematical System Theory. New York: McGraw-Hill.
Kuo, B. C. (1967). Automatic Control Systems. Englewood Cliffs, NJ: Prentice-Hall.
Lefschetz, S. (1965). Stability of nonlinear control systems. In Mathematics in Science and Engineering, vol. 13. London: Academic Press.
Maxwell, J. C. (1868). On governors. Proc. of the Royal Soc. London 16:270-283.
Minorsky, N. (1942). Self-excited oscillations in dynamical systems possessing retarded action. J. of Applied Mechanics 9:65-71.
Nyquist, H. (1932). Regeneration theory. Bell Systems Technical Journal 11:126-147.
Sontag, E. D. (1990). Mathematical Control Theory. New York: Springer.
Willems, J. C. (1986). From time series to linear systems. Automatica 22:561-580.
Copyright © 1999 Massachusetts Institute of Technology