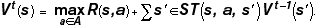
Equation 1
Some problems can be structured into a collection of small problems, each of which can be solved on the basis of the solution of some of the others. The process of working a solution back through the subproblems in order to reach a final answer is called dynamic programming. This general algorithmic technique is applied in a wide variety of areas, from optimizing airline schedules to allocating cell-phone bandwidth to justifying typeset text. Its most common and relevant use, however, is for PLANNING optimal paths through state-space graphs, in order, for example, to find the best routes between cities in a map.
In the simplest case, consider a directed, weighted graph < S, A, T, L>, where S is the set of nodes or "states" of the graph, and A is a set of arcs or "actions" that may be taken from each state. The state that is reached by taking action a in state s is described as T(s,a); the positive length of the a arc from state s is written L(s,a). Let g ∈ S be a desired goal state. Given such a structure, we might want to find the shortest path from a particular state to the goal state, or even to find the shortest paths from each of the states to the goal.
In order to make it easy to follow shortest paths, we will use dynamic programming to compute a distance function, D(s), that gives the distance from each state to the goal state. The ALGORITHM is as follows:
We start by initializing D(s) = large to be an overestimate of the distance between s and g (except in the case of D(g), for which it is exact). Now, we want to improve iteratively the estimates of D(s). The inner loop updates the value for each state s to be the minimum over the outgoing arcs of L(s,a) + D(T(s,a)); the first term is the known distance of the first arc and the second term is the estimated distance from the resulting state to the goal. The outer loop is executed as many times as there are states.
The character of this algorithm is as follows: Initially, only D(g) is correct. After the first iteration, D(s) is correct for all states whose shortest path to the goal is one step long. After |S| iterations, it is correct for all states. Note that if L was uniformly 1, then all the states that are i steps from the goal would have correct D values after the ith iteration; however, it may be possible for some state s to be one step from g with a very long arc, but have a much shorter path with more steps, in which case the D value after the iteration would still be an overestimate.
Once D has been computed, then the optimal path can be described by, at any state s, choosing the action a that minimizes D(a,s). Rather than just a single plan, or trajectory of states, we actually have a policy, mapping every state to its optimal action.
A generalization of the shortest-paths problem is the problem of finding optimal policies for Markov decision processes (MDPs). An MDP is a tuple < S, A, T, R>, where S and A are state and action sets, as before; T(s,a) is a stochastic state-transition function, mapping a state and action into a probability distribution over next states (we will write T(s,a,s´) as the probability of landing in state s´ as a result of taking action a in state s); and R(s,a) is a reward function, describing the expected immediate utility resulting from taking action a in state s. In the simplest case, we seek a policy π that will gain the maximum expected total reward over some finite number of steps of execution, k.
In the shortest-paths problem, we computed a distance function D that allowed us to derive an optimal policy cheaply. In MDPs, we seek a value function Vk(s), which is the expected utility (sum of rewards) of being in state s and executing the optimal policy for k steps. This value function can be derived using dynamic programming, first solving the problem for the situation when there are t steps remaining, then using that solution to solve the problem for the situation when there are t + 1 steps remaining. If there are no steps remaining, then clearly V0(s) = 0 for all s. If we know Vt-1, then we can express V(t) as
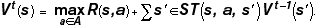
Equation 1
The t-step value of state s is the maximum over all actions (we get to choose the best one) of the immediate value of the action plus the expected t - 1-step value of the next state. Once V has been computed, then the optimal action for state s with t steps to go is the action that was responsible for the maximum value of Vt(s).
Solving MDPs is a kind of planning problem, because it is assumed that a model of the world, in the form of the T and R functions, is known. When the world model is not known, the solution of MDPs becomes the problem of REINFORCEMENT LEARNING, which can be thought of as stochastic dynamic programming.
The theory of dynamic programming, especially as ap-plied to MDPs, was developed by Bellman (1957) and Howard (1960). More recent extensions and developments are described in excellent recent texts by Puterman (1994) and Bertsekas (1995).
Bellman, R. (1957). Dynamic Programming. Princeton, NJ: Princeton University Press.
Bertsekas, D. P. (1995). Dynamic Programming and Optimal Control, vols. 1-2. Belmont, MA: Athena Scientific.
Howard, R. A. (1960). Dynamic Programming and Markov Processes. Cambridge, MA: The MIT Press.
Puterman, M. L. (1994). Markov Decision Processes. New York: John Wiley and Sons.