Figure 1
Depth perception is one of the oldest problems of philosophy and experimental psychology. It has always intrigued people because of the two-dimensionality of the retinal image, although this is not really relevant because, as Descartes (1637) realized, we do not perceive the retinal image. DESCARTES was one of the first to suggest that depth could be computed from changes in the accommodation and convergence of the eyes. Accommodation is the focusing of the lenses and convergence is the inward/outward turning of the eyes stimulated by a change in the distance of the object of regard. Unfortunately, convergence and accommodation vary little beyond a meter or two and we clearly have a sense of depth well beyond that. Cutting and Vishton (1995) note that different cues to depth seem to be operative for near (personal) space, ambient (action) space, and vista (far) space. Convergence and accommodation clearly apply best to the space approximately within arm's reach, but even in that region their effectiveness in giving an impression of absolute distance varies among persons and is imprecise.
Interposition, or the hiding of one object by another, creates an ordinal sense of depth at all distances. But how is interposition specified in visual stimulation? Interposition or occlusion can be indicated monocularly by such contour arrangements as T junctions and alignments (Kanisza 1979) or binocularly by the fact that parts of background objects or regions are hidden from one eye and not the other (Leonardo da Vinci 1505). Current evidence suggests that unlike monocular occlusion cues, binocular occlusion cues can elicit a sense of metric depth (Gillam, Blackburn, and Nakayama 1999).
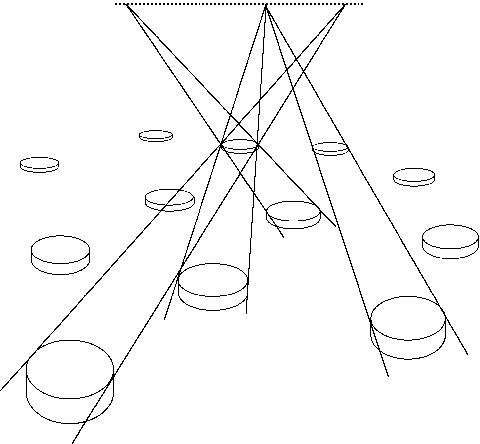
It is generally found that people are quite accurate in judging ambient distance (up to approximately twenty feet). This is typically demonstrated by having them survey the scene, close their eyes, and walk to a predesignated object (Loomis et al. 1992). Perhaps the most important source of distance information in ambient and far space is spatial layout information of the kind first analyzed by James Jerome GIBSON (1950, 1966), although much of the underlying perspective geometry was known by artists of the Renaissance (Alberti 1435). Gibson pointed out that objects are nearly always located on a ground plane and that if the ground is homogeneously textured, it provides a scale in the "optic array" (the projection of the layout to a station point) which can be used to compare distances between elements in any direction at any distance. If the size of the units of texture are known, for example by their relationship to the observer, the scale may also specify absolute distance. In practice it has been found that random dot textures give a much poorer sense of depth than regular textures, especially regular textures that include lines converging toward a vanishing point. Vanishing points and horizons provide depth information in their own right. (A horizon is the locus of the vanishing points of all sets of parallel lines on a planar surface.) For example, the angular extent in the optic array of a location on a surface and the horizon of that surface specifies the absolute distance of that location to a scale factor given by the observer's eye height. Furthermore, the angular distances from two locations on a surface to the horizon can give the relative distances of those locations independently of eye height (Sedgwick 1986). The horizon can be implicitly specified by converging lines even if they do not extend to a vanishing point and also by randomly arranged elements of finite uniform size (see figure 1).

Figure 1
It is generally agreed that the familiar size of isolated objects is not used to derive distance from their angular size although this is possible in principle. However, relative size, especially for objects of a similar shape, is an excellent cue to relative distance. Likewise, an object changing size is normally seen as looming or receding in depth.
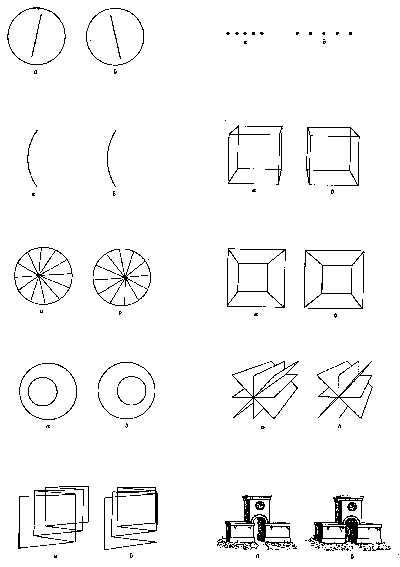
Figure 2
Parallax, defined as the difference in the projection of a static scene as viewpoint changes relative to the scene, is a potent source of information about depth. Motion parallax refers to successive viewpoint changes produced by motion of the observer, whereas binocular parallax refers to the simultaneous differences in viewpoint provided by two horizontally separated eyes. The disparate images thus produced result in "stereoscopic vision." Wheatstone (1838), who discovered stereoscopic vision, showed that the projections of a scene to the two eyes differ in a number of ways (see figure 2), and there is some evidence that the visual system responds directly to certain higher order image differences such as contour orientation. Binocular disparity is usually specified, however, as the difference in the horizontal angles subtended at the two eyes by two points separated in depth.
Stereoscopic vision really comes into its own in near vision where it is important in eye-hand coordination, and in ambient vision where it allows discrete elements that do not provide perspective cues, such as the leaves and branches of a forest, to be seen in vivid relief. The disparity produced by a given depth interval declines rapidly as the distance of the interval from the observer increases. Nevertheless it is possible with moderate stereoscopic acuity to detect that an object at about five hundred meters is nearer than infinity. Because the binocular disparity produced by a given depth interval declines with its distance, the depth response to disparity must be scaled for distance to reflect depth accurately. Scaling has largely been studied at close distances where it is excellent under full cue conditions although it is not yet clear how the scaling is achieved (Howard and Rogers 1995). The accuracy of scaling in vista space is not known. Stereoscopic depth is best for objects that are laterally close to each other (Gogel 1963). At such separations stereoscopic depth is a "hyperacuity" because disparities of only 10-30 sec of arc can be responded to as a depth separation (Westheimer 1979).
Despite the fact that binocular and motion parallax have identical geometry, stereopsis is the superior sense for depth perception under most conditions, especially when there are only two objects separated in depth. Motion parallax is almost as good as stereopsis, however, in eliciting perception of depth in densely patterned corrugated surfaces (Rogers and Graham 1979). A strong sense of solidity is also obtained monocularly when a skeletal object, such as a tangled wire, is rotated in depth and viewed with a stationary eye (kinetic depth effect). The depth variations in densely textured surfaces can also be perceived on the basis of the monocular transformations they undergo during motion.
Many of the possible sources of information about depth have not yet been adequately investigated, especially the sources used in ambient and vista space. There are also unresolved theoretical issues such as the relationship between the apparent distances of objects to the observer and their apparent distances from each other.
Alberti, L. (1435). On Painting. Translated by J. R. Spencer, 1956. New Haven, CT: Yale University Press.
Cutting, J. E., and P. Vishton. (1995). Perceiving layout and knowing distances: The integration, relative potency and contextual use of different information about depth. In W. Epstein and S. Rogers, Eds., Perception of Space and Motion. San Diego: Academic Press, pp. 69-117.
Descartes, R. (1637). Discourse on Method, Optics, Geometry and Meteorology. Translated by Paul J. Olscamp, 1965. Indianapolis: Bobbs-Merrill.
Gibson, J. J. (1950). The Perception of the Visual World. Boston: Houghton Mifflin.
Gibson, J. J. (1966). The Senses Considered as Perceptual Systems. Boston: Houghton Mifflin.
Gillam, B. J., S. Blackburn, and K. Nakayama. (1999). Unpaired background stereopsis: Metrical encoding of depth and slant without matching contours. To appear in Vision Research.
Gogel, W. C. (1963). The visual perception of size and distance. Vision Research 3:101-120.
Howard, I. P., and B. J. Rogers. (1995). Binocular Vision and Stereopsis. New York: Oxford University Press.
Kanisza, G. (1979). Organization in Vision. New York: Praeger.
Leonardo da Vinci. (1505). Codex Manuscript D. In the Bibliothèque Nationale, Paris. English translation in D. S. Strong (1979), Leonardo on the Eye. New York: Garland, pp 41-92.
Loomis, J. M., J. A. Da Silva, N. Fujita, and S. S. Fukusima. (1992). Visual space perception and visually directed action. Journal of Experimental Psychology: Human Perception and Performance 18(4):906-921.
Rogers, B. J., and M. E. Graham. (1979). Motion parallax as an independent cue for depth perception. Perception 8:125-134.
Sedgwick, H. A. (1986). Space perception. In K. Boff, L. Kaufman, and J. Thomas, Eds., Handbook of Perception and Human Performance, vol. 1. New York: John Wiley and Sons.
Westheimer, G. (1979) Cooperative neural processes involved in stereoscopic acuity. Experimental Brain Research 36:585-597.
Wheatstone, C. (1838). Contributions to the physiology of vision: 1. On some remarkable and hitherto unobserved phenomena of binocular vision. Philisophical Transactions of the Royal Society, London 128:371-394.