Quantifiers
Sentences
(Ss) such as All cats are grey consist of a predicate are
grey and a noun phrase (NP) all cats, itself consisting
of a noun cats and a determiner (Det), of which the quantifiers all,
some, and no are special cases. Semantically we treat
both the noun and the predicate as denoting properties of
individuals, and we interpret the S as True in a situation s if
the individuals with those properties (in s) stand in the
relation expressed by the quantifier. Different quantifiers typically
denote different relations. ALL (we write denotations in upper case)
says that the individuals that have the noun property (CAT) are included
in those with the predicate property (GREY). SOME says that the
individuals with the CAT property overlap with those that are GREY;
NO says there is no overlap. EXACTLY TEN says the overlap has exactly
ten members. MOST, in the sense of MORE THAN HALF, expresses a proportion: The
overlap between CAT and GREY is larger than that between CAT and
NON-GREY; that is, the number of grey cats is larger than the number
of non-grey ones. LESS THAN HALF makes the opposite claim.
The role of the noun is crucial.
Syntactically it forms an NP constituent (all cats) with
the quantifier. We interpret this NP as a function, called a generalized
quantifier, that maps the predicate property to True or False
(in a situation). So we interpret All cats are grey by
(ALL CAT)(GREY), where ALL CAT is a function mapping a property P to
True in a situation s if the cats in s are a subset
of the objects with P in s. More generally, Ss
of the form [[Det+N]+Predicate] denote
the truth value given by (D(N))(P), where P is
the property denoted by the predicate, N that denoted by
the noun, D the denotation of the Det, and D(N)
the denotation of Det+noun NP.
Semantically the noun property N serves
to restrict the class of things we are quantifying over.
The literature captures this intuition with two very general constraints
on possible Det denotations. These constraints limit both the logical
expressive power of natural languages and the hypotheses children
need consider in learning the meanings of the Dets in their language
(Clark 1996; see SEMANTICS, ACQUISITION OF).
One condition is extensions (Van
Benthem 1984), which says in effect that the truth of Det Ns
are Ps cannot depend on which individuals are non-Ns. For example,
scouring Old English texts, you will never stumble upon a Det blik that
guarantees that Blik cats are grey is true if and only
if the number of non-cats that are grey is ten.
The second condition is
conservativity (Keenan 1981; Barwise and Cooper 1981; Higginbotham
and May 1981; Keenan and Stavi 1986), which says that the truth
of Det Ns are Ps cannot depend on Ps that lack N. So Det
Ns are Ps must have the same truth value as Det Ns are
Ns that are Ps. For instance, Most cats are grey is
equivalent to Most cats are cats that are grey. And most can
be replaced by any Det, including syntactically complex ones: most
but not all, every child's, or more male than
female. Despite appearances this semantic equivalence is not
trivial. Keenan and Stavi show that in a situation with only two individuals
there are 65,536 logically possible Det denotations (functions from
pairs of properties to truth values). Only 512 of them are conservative!
The restricting role of the noun
property distinguishes natural languages from first-order LOGIC (FOL).
FOL essentially limits its quantifiers to (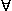 x) every object and
(
x) every object and
(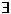 x) some object and forces logical forms to vary
considerably and nonuniformly from the English Ss they represent. All
cats are grey becomes "For all objects x, ifx is
a cat thenx is grey"; Some cats
are grey becomes "For some object x, x is
a cat andx is grey." Now proportionality
quantifiers (most, less than half, a third of the, ten percent
of the) are inherently restricted (Keenan 1993): there
is no Boolean compound S of cat(x) and grey(x) such that (for
most x)S is True if and only if the grey cats outnumber the
non-grey ones. Indeed the proper proportionality Dets are not even
definable in FOL (see Barwise and Cooper (1981) for most),
whence the logical expressive power of natural languages properly extends
that of FOL.
x) some object and forces logical forms to vary
considerably and nonuniformly from the English Ss they represent. All
cats are grey becomes "For all objects x, ifx is
a cat thenx is grey"; Some cats
are grey becomes "For some object x, x is
a cat andx is grey." Now proportionality
quantifiers (most, less than half, a third of the, ten percent
of the) are inherently restricted (Keenan 1993): there
is no Boolean compound S of cat(x) and grey(x) such that (for
most x)S is True if and only if the grey cats outnumber the
non-grey ones. Indeed the proper proportionality Dets are not even
definable in FOL (see Barwise and Cooper (1981) for most),
whence the logical expressive power of natural languages properly extends
that of FOL.
English presents subclasses of Dets
of both semantic and syntactic interest. We note two such: First, simplex (= single
word) Dets satisfy stronger conditions than conservativity and extension.
We say that an NP X is increasing (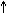 ) if and only if X
is a P (or X are Ps) and all Ps are Qs entails
that X is a Q. Proper names are
) if and only if X
is a P (or X are Ps) and all Ps are Qs entails
that X is a Q. Proper names are 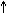 : If all cats are grey and Felix
is a cat, then Felix is grey. An NP of the form [Det+N] is
: If all cats are grey and Felix
is a cat, then Felix is grey. An NP of the form [Det+N] is 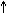 when
Det is every, some, both, most, more than half, at least ten,
infinitely many, or a possessive Det like some boy's whose
possessor NP (some boy) is itself increasing. X is decreasing (
when
Det is every, some, both, most, more than half, at least ten,
infinitely many, or a possessive Det like some boy's whose
possessor NP (some boy) is itself increasing. X is decreasing (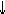 )
if all Ps are Qs and X is a Q entails X is a P. [Det+N] is
)
if all Ps are Qs and X is a Q entails X is a P. [Det+N] is 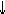 when
Det is no, neither, fewer than ten, less than half, not more
than five, at most five or NP's, for NP
when
Det is no, neither, fewer than ten, less than half, not more
than five, at most five or NP's, for NP 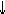 .
X is monotonic if it is either increasing or decreasing. [Det+N] is
non-monotonic if Det equals exactly five, between five and ten,
all but ten, more male than female, at least two and not more than
ten. Simplex Dets build monotonic NPs (usually increasing),
a very proper subset of the NPs of English.
.
X is monotonic if it is either increasing or decreasing. [Det+N] is
non-monotonic if Det equals exactly five, between five and ten,
all but ten, more male than female, at least two and not more than
ten. Simplex Dets build monotonic NPs (usually increasing),
a very proper subset of the NPs of English.
Syntactically note that 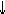 NPs
license negative polarity items in the predicate,
NPs
license negative polarity items in the predicate, 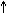 ones do not
(Ladusaw 1983). Thus ever is natural in No/Fewer
than five students here have ever been to Pinsk but not in Some/More
than five students here have ever been to Pinsk. Often, as
here, grammatical properties of NPs are determined by their Dets.
ones do not
(Ladusaw 1983). Thus ever is natural in No/Fewer
than five students here have ever been to Pinsk but not in Some/More
than five students here have ever been to Pinsk. Often, as
here, grammatical properties of NPs are determined by their Dets.
Second, many English Dets are intersective, in
that we determine the truth of Det Ns are Ps just by checking
which Ns are Ps, ignoring Ns that aren't Ps. Most intersective
Dets are cardinal, in that they just depend on how
many Ns are Ps. Some is cardinal: whether Some
Ns are Ps is decided just by checking that the number of Ns
that are Ps is greater than 0. Some other cardinal Dets are no,
(not) more than ten, fewer than/exactly/at most
ten, between five and ten, about twenty, infinitely many and just
finitely many.No . . . but John (as in no student
but John) is intersective but not cardinal. All and most are
not intersective: if we are just given the set of Ns that are Ps
we cannot decide if all or most Ns are Ps.
Intersectivity applies to two-place
Dets like more . . . than . . . that combine with two Ns
to form an NP, as in More boys than girls were drafted. It
is intersective in that the truth of the S is determined once we
are given the intersection of the predicate property with each of the
noun properties. Other such Dets are fewer . . . than . . .
, exactly as many . . . as . . . , more than twice as many . . .
as . . . , the same number of . . . as . . . . In general these
Dets are also not first-order definable (even on finite domains).
Moreover, of syntactic interest, it is the intersective Dets that
build NPs that occur naturally in existential There contexts: There
weren't exactly ten cats/more cats than dogs in
the yard is natural but becomes ungrammatical when exactly ten is
replaced by most or all.
Finally, we can isolate the purely "quantitative" or "logical" Dets
as those whose denotations are invariant under permutations p of
the domain of objects under discussion. So they satisfy D(N)(P)) = D(pN)(pP), where p is
a permutation and p(A) is {p(x)|x 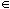 A}. All,
most but not all, just finitely many always denote permutation
invariant functions, but no student's, every . . .
but John, more male than female don't.
A}. All,
most but not all, just finitely many always denote permutation
invariant functions, but no student's, every . . .
but John, more male than female don't.
Cognitive and logical complexity
increases with Ss built from transitive verbs (P2s) and two NPs.
For example Some editor reads every manuscript has two
interpretations: One, there is at least one editor who has the property
that he reads every manuscript; and two, for each manuscript there is
at least one editor who reads it (possibly different editors read
different manuscripts). Cognitively, language acquisition studies
(Lee 1986; Philip 1992) support that children acquire adult-level
competence with such Ss years after they are competent on Ss built
from one-place predicates (P1s). And mathematically, whether a sentence
is logically true is mechanically decidable in first-order languages
with just P1s but loses this property once a single P2 is added
(Boolos and Jeffrey 1989).
But some Ss built from P2s and two
NPs cannot be adequately represented by iterated application of
generalized quantifiers (Keenan 1987, 1992; van Benthem 1989): Different people
like different things; No two students answered exactly the same
questions; John criticized Bill but no one else criticized anyone
else. Adequate intrepretations treat the pair of NPs in each
S as a function mapping the binary relation denoted by the P2 to
a truth value.
Lastly, quantification can also be
expressed outside of Dets and NPs: Students rarely/never/always/often/usually
take naps after lunch (Lewis 1975; Heim 1982; de Swart 1996). Bach
et al. 1995 contains several articles discussing languages in which
non-Det quantification is prominent: Eskimo (Bittner), Mayali (Evans),
or possibly even absent: Straits Salish (Jelinek) and Asurini do
Trocará (Vieira). Recent overviews of Det type quantification
are Keenan (1996) and the more technical Keenan and Westerståhl (1997).
See also
Additional links
-- Edward L. Keenan
References
Bach, E., E. Jelinek, A. Kratzer, and B. Partee,
Eds. (1995). Quantification in Natural Languages. Dordrecht:
Kluwer.
Barwise, J., and R. Cooper. (1981). Generalized
quantifiers and natural language. Linguistics and Philosophy 4:159-219.
Boolos, G., and R. Jeffrey. (1989). Computability
and Logic. 3rd ed. New York: Cambridge University Press.
Clark, R. (1996). Learning first order quantifier
denotations, an essay in semantic learnability. Technical
Reports I.R.C.S. - 96-19, University of Pennsylvania.
de Swart, H. (1996). Quantification over time.
In J. van der Does and J. van Eijck 1996, pp. 311-336.
Gärdenfors, P., Ed. (1987). Generalized
Quantifier: Linguistic and Logical Approaches. Dordrecht: Reidel.
Heim, I. R. (1982). The Semantics of Definite
and Indefinite Noun Phrases. Ph.D. diss., University of Massachusetts, Amherst.
Higginbotham, J., and R. May. (1981). Questions,
quantifiers and crossing. The Linguistic Review 1:41-79.
Keenan, E. L. (1981). A boolean approach to
semantics. In J. Groenendijk et al., Eds., Formal Methods
in the Study of Language. Amsterdam: Math Centre, pp. 343-379.
Keenan, E. L. (1987). Unreducible n-ary
quantifiers in natural language. In P. Gärdenfors (1987).
Keenan, E. L. (1992). Beyond the Frege boundary. Linguistics
and Philosophy 15:199-221. (Augmented and reprinted
in van der Does and van Eijck 1996).
Keenan, E. L. (1993). Natural language, sortal
reducibility, and generalized quantifiers. J. Symbolic Logic 58:314-325.
Keenan, E. L. (1996). The semantics of determiners.
In S. Lappin, Ed., The Handbook of Contemporary Semantic Theory. Oxford:
Blackwell, pp. 41-63.
Keenan, E. L., and J. Stavi. (1986). A semantic
characterization of natural language determiners. Linguistics
and Philosophy 9:253-326.
Keenan, E. L., and D. Westerståhl. (1997).
Generalized quantifiers in linguistics and logic. In J. van Benthem
and A. ter Meulen (1997), pp. 837-893.
Ladusaw, W. (1983). Logical form and conditions
on grammaticality. Linguistics and Philosophy 6:389-422.
Lee, T. (1986). Acquisition of quantificational
scope in Mandarin Chinese. Papers and Reports on Child Language
Development No. 25. Stanford University.
Lewis, D. (1975). Adverbs of quantification.
In E. L. Keenan, Ed., Formal Semantics of Natural Language. Cambridge:
Cambridge University Press, pp. 3-15.
Philip, W. (1992). Distributivity and logical
form in the emergence of universal quantification. In Proceedings
of the Second Conference on Semantics and Linguistic Theory. Ohio
State University Dept. of Linguistics, pp. 327-345.
Szabolcsi, A., Ed. (1997). Ways of Scope
Taking. Dordrecht: Kluwer.
Van Benthem, J. (1984). Questions about quantifiers. J.
Symbolic Logic 49:443-466.
Van Benthem, J. (1989). Polyadic quantifiers. Linguistics
and Philosophy 12:437-465.
Van Benthem, J., and A. ter Meulen, Eds. (1997). The
Handbook of Logic and Language. Amsterdam: Elsevier.
Van der Does, J., and J. van Eijck. (1996).
Quantifiers, logic, and language. CSLI Lecture
Notes. Stanford.
Further Readings
Beghelli, F. (1992). Comparative quantifiers.
In P. Dekker and M. Stokhof, Eds., Proceedings of the Eighth
Amsterdam Colloquium. ILLC, University of Amsterdam.
Cooper, R. (1983). Quantification and
Syntactic Theory. Dordrecht: Reidel.
Gil, D. (1995). Universal quantifiers and distributivity.
In E. Bach et al. 1995, pp. 321-362.
Kanazawa, M., and C. Pion, Eds. (1994). Dynamics,
Polarity and Quantification. Stanford, CA: CSLI Publications,
pp. 119-145.
Kanazawa, M., C. Pion, and H. de Swart, Eds.
(1996). Quantifiers, Deduction and Context. Stanford,
CA: CSLI Publications.
Keenan, E. L., and L. Faltz. (1985). Boolean
Semantics for Natural Language. Dordrecht: Reidel.
Keenan, E. L., and L. Moss. (1985). Generalized
quantifiers and the expressive power of natural language. In van
Benthem and ter Meulen, Eds., Generalized Quantifiers. Dordrecht:
Foris, pp. 73-124.
Lindström, P. (1966). First order predicate
logic with generalized quantifiers. Theoria 35:186-195.
Montague, R. (1969/1974). English as a
formal language. In R. Thomason, Ed., Formal Philosophy. New
Haven, CT: Yale University Press.
Partee, B. H. (1995). Quantificational structures
and compositionality. In Bach et al. 1995, pp. 541-560.
Reuland, E., and A. ter Meulen. (1987). The
Representation of (In)definiteness. Cambridge, MA: MIT Press.
van Benthem, J. (1986). Essays in Logical
Semantics. Dordrecht: Reidel.
Westerståhl, D. (1989). Quantifiers
in formal and natural languages. In D. Gabbay and F. Guenthner, Eds., Handbook
of
Philosophical Logic, vol. 4. Dordrecht: Reidel, pp. 1-131.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
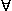 x) every object and
(
x) every object and
(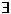 x) some object and forces logical forms to vary
considerably and nonuniformly from the English Ss they represent. All
cats are grey becomes "For all objects x, ifx is
a cat thenx is grey"; Some cats
are grey becomes "For some object x, x is
a cat andx is grey." Now proportionality
quantifiers (most, less than half, a third of the, ten percent
of the) are inherently restricted (Keenan 1993): there
is no Boolean compound S of cat(x) and grey(x) such that (for
most x)S is True if and only if the grey cats outnumber the
non-grey ones. Indeed the proper proportionality Dets are not even
definable in FOL (see Barwise and Cooper (1981) for most),
whence the logical expressive power of natural languages properly extends
that of FOL.
x) some object and forces logical forms to vary
considerably and nonuniformly from the English Ss they represent. All
cats are grey becomes "For all objects x, ifx is
a cat thenx is grey"; Some cats
are grey becomes "For some object x, x is
a cat andx is grey." Now proportionality
quantifiers (most, less than half, a third of the, ten percent
of the) are inherently restricted (Keenan 1993): there
is no Boolean compound S of cat(x) and grey(x) such that (for
most x)S is True if and only if the grey cats outnumber the
non-grey ones. Indeed the proper proportionality Dets are not even
definable in FOL (see Barwise and Cooper (1981) for most),
whence the logical expressive power of natural languages properly extends
that of FOL.
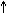 ) if and only if X
is a P (or X are Ps) and all Ps are Qs entails
that X is a Q. Proper names are
) if and only if X
is a P (or X are Ps) and all Ps are Qs entails
that X is a Q. Proper names are 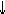 )
if all Ps are Qs and X is a Q entails X is a P. [Det+N] is
)
if all Ps are Qs and X is a Q entails X is a P. [Det+N] is 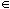 A}. All,
most but not all, just finitely many always denote permutation
invariant functions, but no student's, every . . .
but John, more male than female don't.
A}. All,
most but not all, just finitely many always denote permutation
invariant functions, but no student's, every . . .
but John, more male than female don't.