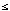 1. Because both
predictions are assumed to follow deductively from T, the probability
calculus implies P (Ds | T) = P (D
o | T) = 1,
and Bayes's theorem yields
1. Because both
predictions are assumed to follow deductively from T, the probability
calculus implies P (Ds | T) = P (D
o | T) = 1,
and Bayes's theorem yields
The ability to formulate coherent and predictive theories of the environment is a salient characteristic of our species. We perform this feat at diverse stages of development and with respect to sundry features of our experience. For example, almost all infants construct grammatical theories of their caretakers' language; most children master the moral and aesthetic codes of their household and community; and selected adults discover scientific principles that govern fundamental aspects of the physical world. In each case, our theories are underdetermined by the data that trigger them in the sense that there exist alternative hypotheses (with different predictive consequences) that are equally compatible with the evidence in hand. In some cases, the underdetermination reaches dramatic proportions, revealed by comparing the fragmentary nature of available data to the scope and apparent accuracy of the theories they engender. Such appears to be the case in the physical sciences. For example, Dodelson, Gates, and Turner (1996) describe a theory of the origin of astrophysical structure, from stars to great walls of galaxies, presenting evidence that such structure arose from quantum mechanical fluctuations during the first 10-34 seconds in the life of the universe. If the theory is true, surely one of its most curious features is that it could be known by a human being. Similarly, radical underdetermination has also been suggested for the grammatical theories constructed by infants learning their first language (for elaboration of this view, see Chomsky 1988 and POVERTY OF THE STIMULUS ARGUMENTS; a critical rejoinder is provided by Pullum 1996; see also INDUCTION and LANGUAGE ACQUISITION).
The psychological processes mediating discovery no doubt vary with the specific problem to which they must apply. There may be little in common, for example, between the neural substrate of grammatical hypotheses and that underlying the conjectures of professional geologists. Such matters are controversial, so it will be prudent to limit the remainder of our discussion to discovery of a patently scientific kind.
The psychological study of discovery has focused on how people choose tests of specific hypotheses, and how they modify hypotheses in the face of confirming or disconfirming data. Many of the experiments are inspired by "Mill's methods" of causal inquiry, referring to the nineteenth-century logician John Stuart Mill. The results suggest that both children and adults are apt to test hypotheses by seeking data that cannot be disconfirmatory, and to retain hypotheses whose predictions are observed to be falsified (see, for example, Kuhn 1996). In contrast to this bleak picture of intuitive science, other researchers believe that Mill's methods are too crude for the framing of pertinent questions about the psychology of empirical inquiry. A different assessment of lay intuition is thought to arise from a subtler account of normative science (see, for example, Koslowski 1996 and SCIENTIFIC THINKING AND ITS DEVELOPMENT).
More generally, investigation of
the psychology of theory discovery can benefit from a convincing
model of rational inquiry, if only to help define the task facing
the reasoner. Two formal perspectives on discovery have been developed
in recent years, both quite primitive but in different ways. One
view focuses on the credibility that scientists attach to alternative theories,
and on the evolution of these credibilities under the impact of
data. Interpreting credibility as probability leads to the
Bayesian analysis of inquiry, which has greatly illuminated
diverse aspects of scientific practice (see BAYESIAN LEARNING).
For example, it is widely acknowledged that a theory T is
better confirmed by data Ds,
which verify a surprising prediction, than by data D
o, which verify an obvious one.
The Bayesian analysis of this fact starts by interpreting surprise probabilistically:
0 < P (Ds) < P
(Do) 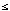 1. Because both
predictions are assumed to follow deductively from T, the probability
calculus implies P (Ds | T) = P (D
o | T) = 1,
and Bayes's theorem yields
1. Because both
predictions are assumed to follow deductively from T, the probability
calculus implies P (Ds | T) = P (D
o | T) = 1,
and Bayes's theorem yields
Equation 1
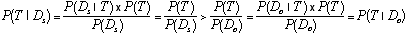
The greater support of T offered by Ds compared to Do is thus explained in terms of the posterior probabilities P(T | D s) and P (T | D o). This example and many others are discussed in Earman (1992), Horwich (1982), Howson and Urbach (1993), and Rosenkrantz (1977).
A second perspective on inquiry is embodied in the "theory of scientific discovery" (see, for example, Kelly 1996; Martin and Osherson 1998; for a computational perspective, see Langley et al. 1987; COMPUTATIONAL LEARNING THEORY; and MACHINE LEARNING). Scientific success here consists not in gradually increasing one's confidence in the true theory, but rather in ultimately accepting it and holding on to it in the face of new data. This way of viewing inquiry is consonant with the philosophy of Karl Popper (1959), and was first studied from an algorithmic point of view in Putnam (1975), Solomonoff (1964), and Gold (1967). Analysis proceeds by distinguishing five components of empirical inquiry, namely: (1) potential realities or "worlds"; (2) a scientific problem; (3) a set of potential data streams or "environments" for each world, which provide information about the world; (4) scientists; and (5) a criterion of success that stipulates the conditions under which a scientist is credited with solving a given problem. Any precise formalization of the preceding items is called a "model" or "paradigm" of inquiry, and may be analyzed mathematically using the techniques developed within the general theory (the five components are adapted from Wexler and Culicover 1980). Particular attention is devoted to characterizing the kinds of problems that can be solved, distinguishing them from problems that resist solution by any scientist.
One of the simplest paradigms to be studied in depth has a numerical character, and may be described as follows (for fuller treatment see Jain et al. forthcoming). Let N be the set {0,1,2, . . .} of natural numbers.
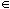 N} of
all subsets of N with just one number missing. A problem
thus specifies a range of theoretically possible worlds, the "real" member
of which must be recognized by the scientist.
N} of
all subsets of N with just one number missing. A problem
thus specifies a range of theoretically possible worlds, the "real" member
of which must be recognized by the scientist.
It is not difficult to see that the scientist S solves the problem P described above. In contrast, it can be demonstrated that no scientist whatsoever solves the problem that results from adding the additional world N to P. This new problem is unsolvable.
The foregoing model of inquiry can be progressively enriched to provide more faithful portraits of science. In one version, worlds are relational structures for a first-order language, scientists implement belief revision operators in the sense of Gärdenfors (1988), and success consists in fixing upon an adequate theory of the structure giving rise to the atomic facts of the environment (see Martin and Osherson 1998).
Chomsky, N. (1988). Language and Problems of Knowledge: The Managua Lectures. Cambridge, MA: MIT Press.
Dodelson, S., E. Gates, and M. Turner. (1996). Cold dark matter. Science 274:69-75.
Earman, J. (1992). Bayes or Bust? Cambridge, MA: MIT Press.
Gärdenfors, P. (1988). Knowledge in Flux: Modeling the Dynamics of Epistemic States. Cambridge, MA: MIT Press.
Gold, E. M. (1967). Language identification in the limit. Information and Control 10:447-474.
Horwich, P. (1982). Probability and Evidence. Cambridge: Cambridge University Press.
Howson, C., and P. Urbach. (1993). Scientific Reasoning: The Bayesian Approach. 2nd ed. La Salle, IL: Open Court.
Jain, S., E. Martin, D. Osherson, J. Royer, and A. Sharma. (Forthcoming). Systems That Learn. 2nd ed. Cambridge, MA: MIT Press.
Kelly, K. T. (1996). The Logic of Reliable Inquiry. New York: Oxford University Press.
Koslowski, B. (1996). Theory and Evidence: The Development of Scientific Reasoning. Cambridge, MA: MIT Press.
Kuhn, D. (1996). Children and adults as intuitive scientists. Psychological Review 96(4).
Langley, P., H. A. Simon, G. L. Bradshaw, and Z. M. Zytkow. (1987). Scientific Discovery. Cambridge, MA: MIT Press.
Martin, E., and D. Osherson. (1998). Elements of Scientific Inquiry. Cambridge, MA: MIT Press.
Popper, K. (1959). The Logic of Scientific Discovery. London: Hutchinson.
Pullum, G. (1996). Learnability, hyperlearning, and the poverty of the stimulus. In J. Johnson, M. L. Juge, and J. L. Moxley, Eds., Proceedings of the Twenty-second Annual Meeting: General Session and Parasession on the Role of Learnability in Grammatical Theory. Berkeley, CA: Berkeley Linguistics Society, pp. 498-513.
Putnam, H. (1975). Probability and confirmation. In Mathematics, Matter and Method. Cambridge: Cambridge University Press.
Rosenkrantz, R. (1977). Inference, Method and Decision. Dordrect: Reidel.
Solomonoff, R. J. (1964). A formal theory of inductive inference. Information and Control 7:1-22, 224 - 254.
Wexler, K., and P. Culicover. (1980). Formal Principles of Language Acquisition. Cambridge, MA: MIT Press .