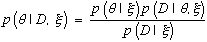
Equation 1
The Bayesian approach views all model learning -- whether of parameters, structure, or both -- as the reduction of a user's UNCERTAINTY about the model given data. Furthermore, it encodes all uncertainty about model parameters and structure as probabilities.
Bayesian learning has two distinct advantages over classical learning. First, it combines prior knowledge and data, as opposed to classical learning, which does not explicitly incorporate user or prior knowledge, so that ad hoc methods are needed to combine knowledge and data (see also MACHINE LEARNING). Second, Bayesian learning methods have a built-in Occam's razor -- there is no need to introduce external methods to avoid overfitting (see Heckerman 1995).
To illustrate with an example taken from Howard 1970, consider a common thumbtack -- one with a round, flat head that can be found in most supermarkets. If we toss the thumbtack into the air, it will come to rest either on its point (heads) or on its head (tails). Suppose we flip the thumbtack N + 1 times, making sure that the physical properties of the thumbtack and the conditions under which it is flipped remain stable over time. From the first N observations, we want to determine the probability of heads on the (N + 1)th toss.
In a classical analysis of this problem, we assert that there is some true probability of heads, which is unknown. We estimate this true probability from the N observations using criteria such as low bias and low variance. We then use this estimate as our probability for heads on the (N + 1)th toss. In the Bayesian approach, we also assert that there is some true probability of heads, but we encode our uncertainty about this true probability using the rules of probability to compute our probability for heads on the (N + 1)th toss.
To undertake a Bayesian analysis of this problem, we need some notation. We denote a variable by an uppercase letter (e.g., X, Xi, Θ), and the state or value of a corresponding variable by that same letter in lowercase (e.g., x, xi, θ). We denote a set of variables by a boldface uppercase letter (e.g., X, Xi, Θ). We use a corresponding boldface lowercase letter (e.g., x, xi, θ) to denote an assignment of state or value to each variable in a given set. We use p(X = x | ξ), or p(x | ξ) as a shorthand, to denote the probability that X = x of a person with state of information ξ. We also use p(x | ξ) to denote the probability distribution for X (both mass functions and density functions). Whether p(x | ξ) refers to a probability, a probability density, or a probability distribution will be clear from context.
Returning to the thumbtack problem, we define Θ to be a variable whose values θ correspond to the possible true values of the probability of heads. We express the uncertainty about Θ using the probability density function p(θ | ξ). In addition, we use X1 to denote the variable representing the outcome of the lth flip, l = 1, . . . , N + 1, and D = {X1 = x1, . . . , XN = xN} to denote the set of our observations. Thus, in Bayesian terms, the thumbtack problem reduces to computing p(xN+1 | D, ξ) from p(θ | ξ).
To do so, we first use Bayes's rule to obtain the probability distribution for Θ given D and background knowledge ξ:
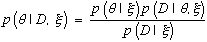
Equation 1
where
p(D | ξ) = ∫ p(D | θ, ξ) p(θ | ξ) dθ
Equation 2
Next, we expand the likelihood p(D | θ, ξ). Both Bayesians and classical statisticians agree on this term. In particular, given the value of Θ, the observations in D are mutually independent, and the probability of heads (tails) on any one observation is θ(1 - θ). Consequently, equation 1 becomes
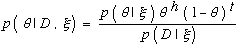
Equation 3
where h and t are the number of heads and tails observed in D, respectively. The observations D represent a random sample from the binomial distribution parameterized by θ; the probability distributions p(θ | ξ) and p(θ | D, ξ) are commonly referred to as the "prior" and "posterior" for Θ, respectively; and the quantities h and t are said to be "sufficient statistics" for binomial sampling because they summarize the data sufficiently to compute the posterior from the prior.
To determine the probability that the (N+1)th toss of the thumbtack will come up heads, we use the expansion rule of probability to average over the possible values of Θ:
| p(XN+1 = heads | D, ξ) |
| = ∫ p(XN+1 = heads | (θ, ξ) p(θ | D, ξ) dθ |
| = ∫ θ p(θ | D, ξ) dθ ≡ Ep(θ | D, ξ)(θ) |
Equation 4
where Ep(θ | D, x)(θ) denotes the expectation of θ with respect to the distribution p(θ | D, ξ).
To complete the Bayesian analysis for this example, we need a method to assess the prior distribution for Θ. A common approach, usually adopted for convenience, is to assume that this distribution is a beta distribution:
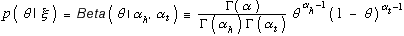
Equation 5
where αh > 0 and αt > 0 are the parameters of the beta distribution, α = αh + αt, and Γ(·) is the gamma function that satisfies Γ(x + 1) = x Γ(x) and Γ(1) = 1. The quantities αh and αt are often referred to as "hyperparameters" to distinguish them from the parameter θ. The hyperparameters αh and αt must be greater than zero so that the distribution can be normalized. Examples of beta distributions are shown in figure 1.
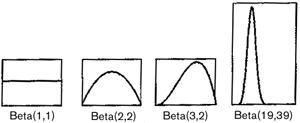
Figure 1.Several beta distributions.
The beta prior is convenient for several reasons. By equation 3, the posterior distribution will also be a beta distribution:
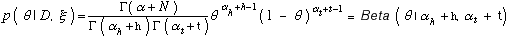
Equation 6
We term the set of beta distributions a conjugate family of distributions for binomial sampling. Also, the expectation of θ with respect to this distribution has a simple form:
∫ θ Beta(θ | αh, αt) dθ = αh/α
Equation 7
Hence, given a beta prior, we have a simple expression for the probability of heads in the (N + 1)th toss:
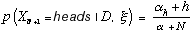
Equation 8
Assuming p(θ|ξ) is a beta distribution, it can be assessed in a number of ways. For example, we can assess our probability for heads in the first toss of the thumbtack (e.g., using a probability wheel). Next, we can imagine having seen the outcomes of k flips, and reassess our probability for heads in the next toss. From equation 8, we have, for k = 1,
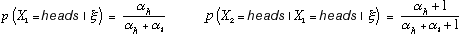
Given these probabilities, we can solve for αh and αt. This assessment technique is known as "the method of imagined future data." Other techniques for assessing beta distributions are discussed by Winkler (1967).
Although the beta prior is convenient, it is not accurate for some problems. For example, suppose we think that the thumbtack may have been purchased at a magic shop. In this case, a more appropriate prior may be a mixture of beta distributions -- for example,
p(θ|ξ) = 0.4 Beta(20, 1) + 0.4 Beta(1, 20) + 0.2 Beta(2, 2)
where 0.4 is our probability that the thumbtack is heavily weighted toward heads (tails). In effect, we have introduced an additional hidden or unobserved variable H, whose states correspond to the three possibilities: (1) thumbtack is biased toward heads, (2) thumbtack is biased toward tails, or (3) thumbtack is normal; and we have asserted that θ conditioned on each state of H is a beta distribution. In general, there are simple methods (e.g., the method of imagined future data) for determining whether or not a beta prior is an accurate reflection of one's beliefs. In those cases where the beta prior is inaccurate, an accurate prior can often be assessed by introducing additional hidden variables, as in this example.
So far, we have only considered observations drawn from a binomial distribution. To be more general, suppose our problem domain consists of variables X = (X1, . . . , Xn). In addition, suppose that we have some data D = (x1, . . . , xN), which represent a random sample from some unknown (true) probability distribution for X. We assume that the unknown probability distribution can be encoded by some statistical model with structure m and parameters θm. Uncertain about the structure and parameters of the model, we take the Bayesian approach -- we encode this uncertainty using probability. In particular, we define a discrete variable M, whose states m correspond to the possible true models, and encode our uncertainty about M with the probability distribution p(m | ξ). In addition, for each model structure m, we define a continuous vector-valued variable Θm, whose configurations θm correspond to the possible true parameters. We encode our uncertainty about Θm using the probability density function p(θm | m, ξ).
Given random sample D, we compute the posterior distributions for each m and θm using Bayes's rule:
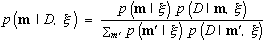
Equation 9
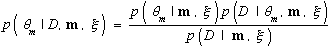
Equation 10
where
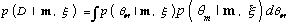
Equation 11
is the marginal likelihood. Given some hypothesis of interest, h, we determine the probability that h is true given data D by averaging over all possible models and their parameters according to the rules of probability:
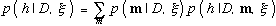
Equation 12
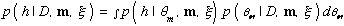
Equation 13
For example, h may be the event that the next observation is x N+1. In this situation, we obtain
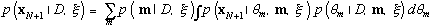
Equation 14
where p(x N+1 | θm, m, ξ) is the likelihood for the model. This approach is often referred to as "Bayesian model averaging." Note that no single model structure is learned. Instead, all possible models are weighted by their posterior probability.
Under certain conditions, the parameter posterior and marginal likelihood can be computed efficiently and in closed form. For example, such computation is possible when the likelihood is given by a BAYESIAN NETWORK (e.g., Heckerman 1998) and several other conditions are met. See Bernardo and Smith 1994, Laurtizen 1996, and Heckerman 1998 for a discussion.
When many model structures are possible, the sums in equations 9 and 12 can be intractable. In such situations, we can search for one or more model structures with large posterior probabilities, and use these models as if they were exhaustive -- an approach known as "model selection." Examples of search methods applied to Bayesian networks are given by Heckerman, Geiger, and Chickering (1995) and Madigan et al. (1996).
Bernardo, J., and A. Smith. (1994). Bayesian Theory. New York: Wiley.
Heckerman, D. (1998). A tutorial on learning with Bayesian networks. In M. Jordan, Ed., Learning in Graphical Models. Kluwer, pp. 301-354
Heckerman, D., D. Geiger, and D. Chickering. (1995). Learning Bayesian networks: The combination of knowledge and statistical data. Machine Learning 20:197-243.
Howard, R. (1970). Decision analysis: Perspectives on inference, decision, and experimentation. Proceedings of the IEEE 58:632-643.
Lauritzen, S. (1996). Graphical Models. Oxford: Clarendon Press.
Madigan, D., A. Raftery, C. Volinsky, and J. Hoeting. (1996). Bayesian model averaging. Proceedings of the AAAI Workshop on Integrating Multiple Learned Models. Portland, OR.
Winkler, R. (1967). The assessment of prior distributions in Bayesian analysis. American Statistical Association Journal 62:776-800 .