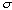 in the language of P,
such that neither s nor its negation ¬
in the language of P,
such that neither s nor its negation ¬ 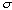 is provable in P.
is provable in P.
Kurt Gödel was one of the most influential logicians of the twentieth century. He established a number of absolutely central facts, among them the semantic completeness of first order logic and the relative consistency of the axiom of choice and of the generalized continuum hypothesis. However, the theorems that have been most significant -- for the general discussion concerning the foundations of mathematics -- are his two incompleteness theorems published in 1931; they are also referred to simply as Gödel's theorems or the Gödel theorems.
The early part of the twentieth century saw a dramatic development of logic in the context of deep problems in the foundations of mathematics. This development provided for the first time the basic means to reflect mathematical practice in formal theories; see FORMAL SYSTEMS. One fundamental question was: Is there a formal theory such that mathematical truth is co-extensive with provability in that theory? Russell's type theory P of Principia Mathematica and axiomatic set theory as formulated by Zermelo seemed to make a positive answer plausible. A second question emerged from the research program that had been initiated by Hilbert around 1920 (with roots going back to the turn of the century): Is the consistency of mathematics in its formalized presentation provable by restricted mathematical, so-called finitist means? The incompleteness theorems gave negative answers to both questions for the particular theories mentioned. To be more precise, a negative answer to the second question is provided only if finitist mathematics itself can be formalized in these theories; that was not claimed by Gödel in 1931, only in his (1933) did he assert it with great force.
The first incompleteness theorem states (making use of an improvement due to Rosser):
If P is consistent, then there is a sentence 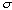 in the language of P,
such that neither s nor its negation ¬
in the language of P,
such that neither s nor its negation ¬ 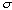 is provable in P.
is provable in P.
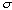 is thus
independent of P. As s is a number theoretic
statement it is either true or false for the natural numbers; in
either case, we have a statement that is true and not provable in
P. This incompleteness of Pcannot be remedied by
adding the true statement to Pas an axiom: for the theory so
expanded, the same incompleteness phenomenon arises.
is thus
independent of P. As s is a number theoretic
statement it is either true or false for the natural numbers; in
either case, we have a statement that is true and not provable in
P. This incompleteness of Pcannot be remedied by
adding the true statement to Pas an axiom: for the theory so
expanded, the same incompleteness phenomenon arises.
Gödel's
second theorem claims the unprovability of a (meta-) mathematically
meaningful statement:
If P is consistent, then cons,the statement in the language of Pthat expresses the consistency of P,is not provable in P.
Some, for example Church, raised the question whether the proofs in some way depended on special features of P. In his Princeton lectures of 1934, Gödel tried to present matters in a more general way; he succeeded in addressing Church's concerns, but continued to strive for even greater generality in the formulation of the theorems. To understand in what direction, we first review the very basic ideas underlying the proofs and then discuss why Turing's work is essential for a general formulation.
Crucial are
the effective presentation of P's syntax and its
(internal) representation. Gödel uses a presentation by
primitive recursive functions, that is, the basic syntactic objects
(strings of letters of P's alphabet and strings of such
strings) are "coded" as natural numbers, and the subsets corresponding
to formulas and proofs are given by primitive recursive characteristic
functions. Representability conditions are established for all
syntactic notions R, that is, really for all primitive
recursive sets (and relations): if R(m) holds then P
proves r (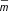 ),and if not
R(m) holds then P proves ¬r(
),and if not
R(m) holds then P proves ¬r(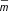 ),where r is a formula in the
language of P and
),where r is a formula in the
language of P and 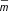 the
numeral for the natural number m. Thus, the metamathematical
talk about the theory can be represented within it. Then the
self-referential statement
the
numeral for the natural number m. Thus, the metamathematical
talk about the theory can be represented within it. Then the
self-referential statement 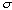 (in the language of P)
is constructed in conscious analogy to the liar sentence;
(in the language of P)
is constructed in conscious analogy to the liar sentence;
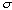 expresses that it
is not provable in P. An argument similar to that showing the
liar sentence not to be true establishes that
expresses that it
is not provable in P. An argument similar to that showing the
liar sentence not to be true establishes that 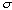 is not provable in P,
thus we have part of the first theorem. The second theorem is
obtained, very roughly speaking, by formalizing the proof of the first
theorem concerning
is not provable in P,
thus we have part of the first theorem. The second theorem is
obtained, very roughly speaking, by formalizing the proof of the first
theorem concerning 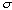 , but additional derivability
conditions are needed: this yields a proof in P of (cons
, but additional derivability
conditions are needed: this yields a proof in P of (cons 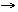
 ). Now, clearly, cons cannot be
provable in P, otherwise s were provable, contradicting the
part of the first theorem we just established. The proof of the
second theorem was given in detail only by Hilbert and Bernays
(1939). A gem of an informal presentation of this material is
(Gödel 1931b); for a good introduction to the mathematical
details see Smorynski (1977).
). Now, clearly, cons cannot be
provable in P, otherwise s were provable, contradicting the
part of the first theorem we just established. The proof of the
second theorem was given in detail only by Hilbert and Bernays
(1939). A gem of an informal presentation of this material is
(Gödel 1931b); for a good introduction to the mathematical
details see Smorynski (1977).
Gödel viewed in (1934) the primitive recursiveness of the syntactic notions as "a precise condition which in practice suffices as a substitute for the unprecise requirement . . . that the class of axioms and relation of immediate consequence be constructive," that is, have an effectively calculable characteristic function. What was needed, in principle, was a precise concept capturing the informal notion of an effectively calculable function, and that would allow a perfectly general characterization of formal theories. Such a notion emerged from the investigations of Church and TURING; see CHURCH-TURING THESIS. Only then was it possible to state and prove the Incompleteness Theorems for all formal theories satisfying representability (for all recursive relations) and derivability conditions. In the above statement of the theorems, the premise "P is consistent" can now be replaced by "P is any consistent formal theory satisfying the representability conditions," respectively "P is any consistent formal theory satisfying the representability and derivability conditions." It is this generality of his results that Gödel emphasized again and again; for example, in his (1964) work: "In consequence of later advances, in particular of the fact that, due to A. M. Turing's work, a precise and unquestionably adequate definition of the general concept of formal system can now be given, the existence of undecidable arithmetical propositions and the non-demonstrability of the consistency of a system in the same system can now be proved rigorously for every consistent formal system containing a certain amount of finitary number theory."
Gödel exploited this general formulation of his theorems (based on Turing's work) and analyzed their broader significance for the philosophy of mathematics and mind most carefully in (1951). The first section is devoted to a discussion of the Incompleteness Theorems, in particular of the second theorem, and argues for a "mathematically established fact" which is of "great philosophical interest" to Gödel: either the humanly evident axioms of mathematics cannot be comprised by a finite rule given by a Turing machine, or they can be and thus allow the successive development of all of demonstrable mathematics. In the latter case human mathematical abilities are in principle captured by a Turing machine, and thus there will be absolutely undecidable problems. That is what can be strictly inferred from Gödel's theorems, counter to Lucas, Penrose, and others. Gödel thought that the first disjunct held, as he believed that the second disjunct had to be false; he emphasized repeatedly, for example in (1964), that his results do not establish "any bounds for the powers of human reason, but rather for the potentialities of pure formalism in mathematics." Indeed, in the Gibbs lecture Gödel reformulated the first disjunct as this dramatic and vague statement: "the human mind (even within the realm of pure mathematics) infinitely surpasses the powers of any finite machine."
Gödel, K. (1931a). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Translated in Collected Works I, pp. 144-195.
Gödel, K. (1931b). Über unentscheidbare Sätze. Translated in Collected Works III, pp. 30-35.
Gödel, K. (1933). The present situation in the foundations of mathematics. In Collected Works III, pp. 45-53.
Gödel, K. (1934). On undecidable propositions of formal mathematical systems (Princeton Lectures). In Collected Works I, pp. 346-369.
Gödel, K. (1951). Some basic theorems on the foundations of mathematics and their implications (Gibbs Lecture). In Collected Works III, pp. 304-323.
Gödel, K. (1964). Postscriptum to Gödel (1934). In Collected Works I, pp. 369-371.
Gödel, K. (1986). Collected Works I. Oxford: Oxford University Press.
Gödel, K. (1990). Collected Works II. Oxford: Oxford University Press.
Gödel, K. (1995). Collected Works III. Oxford: Oxford University Press.
Hilbert, D. and P. Bernays. (1939). Grundlagen der Mathematik II. Berlin: Springer.
Lucas, J. R. (1961). Minds, machines and Gödel. Philosophy 36:112-127.
Penrose, R. (1989). The Emperor's New Mind. New York: Oxford University Press.
Rosser, B. (1936). Extensions of some theorems of Gödel and Church. J. Symbolic Logic 2:129-137.
Smorynski, C. (1977). The incompleteness theorem. In J. Barwise, Ed., Handbook of Mathematical Logic. Amsterdam. North-Holland, pp. 821-865.
Dawson, J. W. (1997). Logical Dilemmas -- The Life and Work of Kurt Gödel. New York: A. K. Peters.