Two very different insights motivate characterizing the brain as a computer. The first and more fundamental assumes that the defining function of nervous systems is representational; that is, brain states represent states of some other system -- the outside world or the body itself -- where transitions between states can be explained as computational operations on representations. The second insight derives from a domain of mathematical theory that defines computability in a highly abstract sense.
The mathematical approach is based on the idea of a Turing machine. Not an actual machine, the Turing machine is a conceptual way of saying that any well-defined function could be executed, step by step, according to simple "if you are in state P and have input Q then do R" rules, given enough time (maybe infinite time; see COMPUTATION). Insofar as the brain is a device whose input and output can be characterized in terms of some mathematical function -- however complicated -- then in that very abstract sense, it can be mimicked by a Turing machine. Because neurobiological data indicate that brains are indeed cause-effect machines, brains are, in this formal sense, equivalent to a Turing machine (see CHURCH-TURING THESIS). Significant though this result is mathematically, it reveals nothing specific about the nature of mind-brain representation and computation. It does not even imply that the best explanation of brain function will actually be in computational/representational terms. For in this abstract sense, livers, stomachs, and brains -- not to mention sieves and the solar system -- all compute. What is believed to make brains unique, however, is their evolved capacity to represent the brain's body and its world, and by virtue of computation, to produce coherent, adaptive motor behavior in real time. Precisely what properties enable brains to do this requires empirical, not just mathematical, investigation.
Broadly speaking, there are two main approaches to addressing the substantive question of how in fact brains represent and compute. One exploits the model of the familiar serial, digital computer, where representations are symbols, in somewhat the way sentences are symbols, and computations are formal rules (algorithms) that operate on symbols, rather like the way that "if-then" rules can be deployed in formal logic and circuit design. The second approach is rooted in neuroscience, drawing on data concerning how the cells of the brain (neurons) respond to outside signals such as light and sound, how they integrate signals to extract high-order information, and how later stage neurons interact to yield decisions and motor commands. Although both approaches ultimately seek to reproduce input-output behavior, the first is more "top-down," relying heavily on computer science principles, whereas the second tends to be more "bottom-up," aiming to reflect relevant neurobiological constraints. A variety of terms are commonly used in distinguishing the two: algorithmic computation versus signal processing; classical artificial intelligence (AI) versus connectionism; AI modeling versus neural net modeling.
For some problems the two approaches can complement each other. There are, however, major differences in basic assumptions that result in quite different models and theoretical foci. A crucial difference concerns the idea of levels. In 1982, David MARR characterized three levels in nervous systems. That analysis became influential for thinking about computation. Based on working assumptions in computer science, Marr's proposal delineated (1) the computational level of abstract problem analysis wherein the task is decomposed according to plausible engineering principles; (2) the level of the ALGORITHM, specifying a formal procedure to perform the task, so that for a given input, the correct output results; and (3) the level of physical implementation, which is relevant to constructing a working device using a particular technology. An important aspect of Marr's view was the claim that a higher level question was independent of levels below it, and hence that problems of levels 1 and 2 could be addressed independently of considering details of the implementation (the neuronal architecture). Consequently, many projects in AI were undertaken on the expectation that the known parallel, analog, continuously adapting, "messy" architecture of the brain could be ignored as irrelevant to modeling mind/brain function.
Those who attacked problems of cognition from the perspective of neurobiology argued that the neural architecture imposes powerful constraints on the nature and range of computations that can be performed in real time. They suggested that implementation and computation were much more interdependent than Marr's analysis presumed. For example a visual pattern recognition task can be performed in about 300 milliseconds (msec), but it takes about 5-10 msec for a neuron to receive, integrate, and propagate a signal to another neuron. This means that there is time for no more than about 20 - 30 neuronal steps from signal input to motor output. Because a serial model of the task would require many thousands of steps, the time constraints imply that the parallel architecture of the brain is critical, not irrelevant.
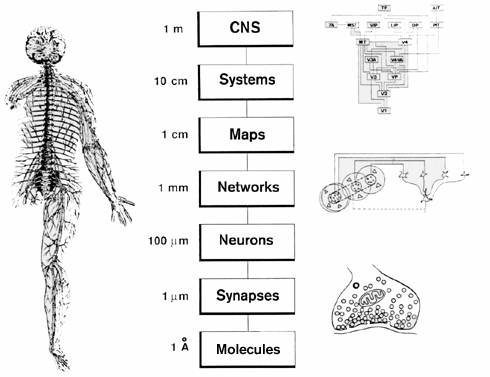
Marr's tripartite division itself was challenged on grounds that nervous systems display not a single level of "implementation," but many levels of structured organization, from molecules to synapses, neurons, networks, and so forth (Churchland and Sejnowski 1992; fig. 1). Evidence indicates that various structural levels have important functional capacities, and that computation might be carried out not only at the level of the neuron, but also at a finer grain, namely the dendrite, as well as at a larger grain, namely the network. From the perspective of neuroscience, the hardware/software distinction did not fall gracefully onto brains.

Figure 1 Diagram showing the major levels of organization of the nervous system.
What, in neural terms, are representations? Whereas the AI approach equates representations with symbols, a term well defined in the context of conventional computers, connectionists realized that "symbol" is essentially undefined in neurobiological contexts. They therefore aimed to develop a new theory of representation suitable to neurobiology. Thus they hypothesized that occurrent representations (those happening now) are patterns of activation across the units in a neural net, characterized as a vector, <x, y, z, . . .>, where each element in the vector specifies the level of activity in a unit. Stored representations, by contrast, are believed to depend on the configuration of weights between units. In neural terms, these weights are the strength of synaptic connections between neurons.
Despite considerable progress, exactly how brains represent and compute remains an unsolved problem. This is mainly because many questions about how neurons code and decode information are still unresolved. New techniques in neuroscience have revealed that timing of neuronal spikes is important in coding, but exactly how this works or how temporally structured signals are decoded is not understood.
In exploring the properties of nervous systems, artificial NEURAL NETWORKS (ANNs) have generally been more useful to neuroscience than AI models. A useful strategy for investigating the functional role of an actual neural network is to train an ANN to perform a similar information processing task, then to analyze its properties, and then compare them to the real system. For example, consider certain neurons in the parietal cortex (area 7a) of the brain whose response properties are correlated with the position of the visual stimulus relative to head-centered coordinates. Since the receptor sheets (RETINA, eye muscles) cannot provide that information directly, it has to be computed from various input signals. Two sets of neurons project to these cells: some represent the position of the stimulus on the retina, some represent the position of the eyeball in the head. Modeling these relationships via an artificial neural net shows how the eyeball/retinal position can be used to compute the position of the stimulus relative to the head (see OCULOMOTOR CONTROL). Once trained, the network's structure can be analyzed to determine how the computation was achieved, and this may suggest neural experiments (Andersen 1995; see also COMPUTATIONAL NEUROSCIENCE).
How biologically realistic to make an ANN depends on the purposes at hand, and different models are useful for different purposes. At certain levels and for certain purposes, abstract, simplifying models are precisely what is needed. Such a model will be more useful than a model slavishly realistic with respect to every level, even the biochemical. Excessive realism may mean that the model is too complicated to analyze or understand or run on the available computers. For some projects such as modeling language comprehension, less neural detail is required than for other projects, such as investigating dendritic spine dynamics.
Although the assumption that nervous systems compute and represent seems reasonable, the assumption is not proved and has been challenged. Stressing the interactive and time-dependent nature of nervous systems, some researchers see the brain together with its body and environment as dynamical systems, best characterized by systems of differential equations describing the temporal evolution of states of the brain (see DYNAMIC APPROACHES TO COGNITION, and Port and van Gelder 1995). In this view both the brain and the liver can have their conduct adequately described by systems of differential equations. Especially in trying to explain the development of perceptual motor skills in neonates, a dynamical systems approach has shown considerable promise (Thelen and Smith 1994).
The main reason for adhering to a framework with computational resources derives from the observation that neurons represent various nonneural parameters, such as head velocity or muscle tension or visual motion, and that complex neuronal representations have to be constructed from simpler ones. Recall the example of neurons in area 7a. Their response profiles indicate that they represent the position of the visual stimulus in head-centered coordinates. Describing causal interactions between these cells and their input signals without specifying anything about representational role masks their function in the animal's visual capacity. It omits explaining how these cells come to represent what they do. Note that connectionist models can be dynamical when they include back projections, time constants for signal propagation, channel open times, as well as mechanisms for adding units and connections, and so forth.
In principle, dynamical models could be supplemented with representational resources in order to achieve more revealing explanations. For instance, it is possible to treat certain parameter settings as inputs, and the resultant attractor as an output, each carrying some representational content. Furthermore, dynamical systems theory easily handles cases where the "output" is not a single static state (the result of a computation), but is rather a trajectory or limit cycle. Another approach is to specify dynamical subsystems within the larger cognitive system that function as emulators of external domains, such as the task environment (see Grush 1997). This approach embraces both the representational characterization of the inner emulator (it represents the external domain), as well as a dynamical system's characterization of the brain's overall function.
Andersen, R. A. (1995). Coordinate transformations and motor planning in posterior parietal cortex. In M. Gazzaniga, Ed., The Cognitive Neurosciences. Cambridge, MA: MIT Press.
Churchland, P. S., and T. J. Sejnowski. (1992). The Computational Brain. Cambridge, MA: MIT Press.
Grush, R. (1997). The architecture of representation. Philosophical Psychology 10(1):5-25.
Marr, D. (1982). Vision. New York: Freeman.
Port, R., and T. van Gelder. (1995). Mind as Motion: Explorations in the Dynamics of Cognition. Cambridge, MA: MIT Press.
Thelen, E., and L. B. Smith. (1994). A Dynamical Systems Approach to the Development of Cognition and Action. Cambridge, MA: MIT Press.
Abeles, M. (1991). Corticonics: Neural Circuits of the Cerebral Cortex. Cambridge: Cambridge University Press.
Arbib, A. M. (1995). The Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press.
Boden, M. (1988). Computer Models of the Mind. Cambridge: Cambridge University Press.
Churchland, P. (1995). The Engine of Reason, the Seat of the Soul. Cambridge, MA: MIT Press.
Koch, C., and I. Segev. (1997). Methods in Neuronal Modeling: From Synapses to Networks. 2nd ed. Cambridge, MA: MIT Press.
Sejnowski, T. (1997). Computational neuroscience. Encyclopedia of Neuroscience. Amsterdam: Elsevier Science Publishers.