The term Categorial Grammar (CG) refers to a group of theories of natural language syntax and semantics in which the main responsibility for defining syntactic form is borne by the LEXICON. CG is therefore one of the oldest and purest examples of a class of lexicalized theories of grammar that also includes HEAD-DRIVEN PHRASE STRUCTURE GRAMMAR, LEXICAL FUNCTIONAL GRAMMAR, Tree-adjoining grammar, Montague grammar, RELATIONAL GRAMMAR, and certain recent versions of the Chomskean theory.
The various modern versions of CG are characterized by a much freer notion of derivational syntactic structure than is assumed under most other formal or generative theories of grammar. All forms of CG also follow Montague (1974) in sharing a strong commitment to the Principle of COMPOSITIONALITY -- that is, to the assumption that syntax and interpretation are homomorphically related and may be derived in tandem. Significant contributions have been made by Categorial Grammarians to the study of SEMANTICS, SYNTAX, MORPHOLOGY, intonational phonology, COMPUTATIONAL LINGUISTICS, and human SENTENCE PROCESSING.
There have been two styles of formalizing the grammar of natural languages since the problem was first articulated in the 1950s. Chomsky (1957) and much subsequent work in GENERATIVE GRAMMAR begins by capturing the basic facts of English constituent order exemplified in (1) in a Context-free Phrase Structure grammar (CFPSG) or system of rewrite rules or "productions" like (2), which have their origin in early work in recursion theory by Post, among others.
Categorial Grammar (CG), together with its close cousin Dependency Grammar (which also originated in the 1950s, in work by Tesnière), stems from an alternative approach to the context-free grammar pioneered by Bar-Hillel (1953) and Lambeck (1958), with earlier antecedents in Ajdukiewicz (1935) and still earlier work by Husserl and Russell in category theory and the theory of types. Categorial Grammars capture the same information by associating a functional type or category with all grammatical entities. For example, all transitive verbs are associated via the lexicon with a category that can be written as follows:
The notation here is the "result leftmost" notation according to which α/β and α/β represent functions from β into α, where the slash determines that the argument β is respectively to the right (/) or to the left (\) of the functor. Thus the transitive verb (3) is a functor over NPs to its right-yielding predicates, or functors over NPs to the left, which in turn yield S. (There are several other notations for categorial grammars, including the widely used "result on top" notation of Lambek 1958 and much subsequent work, according to which the above category is written (NP\S)/NP. The advantage of the present notation for cognitive scientists is that semantic type can be read in a consistent left-right order, regardless of directionality.)
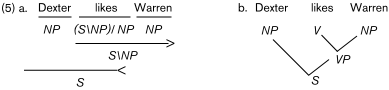
In "pure" context-free CG, categories can combine via two general function application rules, which in the present notation are written as in (4), to yield derivations, written as in (5a), in which underlines indexed with right and left arrows indicate the application of the two rules.

Such derivations are equivalent to traditional trees like (5b) in CFPSG. However, diagrams like (5a) should be thought of as derivations, delivering a compositional interpretation directly, rather than a purely syntactic structure. The identification of derivation with interpretation becomes important when we consider the extensions of CG that take it beyond weak equivalence with CFPSG.
A central problem for any theory of grammar is to capture the fact that elements of sentences that belong together at the level of semantics or interpretation may be separated by much intervening material in sentences, the most obvious example in English arising from the relative clause construction. All theories of grammar respond to this problem by adding something such as the transformationalists' WH-MOVEMENT, GPSG feature-passing, ATN HOLD registers, or whatever to a context-free core. Usually, such additions increase automata-theoretic power. To the extent that the constructions involved seem to be quite severely constrained, and that certain kinds of long-range dependencies seem to be universally prohibited, there is clearly some explanatory value in keeping such power to a minimum.
All of the generalizations of categorial grammar respond to this problem by adding various type-driven combinatory operators to pure CG. The many different proposals for how to do this fall under two quite distinct approaches. The first, rule-based, approach, pioneered by Lyons (1968), Bach (1976), and Dowty (1979), among other linguists, and by Lewis (1970) and Geach (1972), among philosophical logicians, starts from the pure CG of Bar-Hillel, and adds rules corresponding to simple operations over categories, such as "wrap" (or commutation of arguments), "type-raising," (which resembles the application of traditional nominative, accusative, etc. case to NPs, etc.) and functional composition. One possible derivation of a complex relative clause comes out as follows in one fairly typical version, "Combinatory" Categorial Grammar (CCG), discussed at length by the present author (see "Further Reading"), in which type-raising and composition are for historical reasons indicated by T and B, respectively.
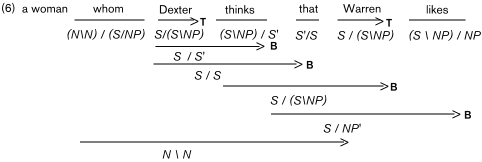
Notice that this analysis bears no resemblance to a traditional right-branching clause structure modified by structure-preserving movement transformations.
The alternative, deductive, style of Categorial Grammar, pioneered by van Benthem (1986) and Moortgat (1988), takes as its starting point Lambek's syntactic calculus. The Lambek system embodies a view of the categorial slash as a form of logical implication for which a number of axioms or inference rules define a proof theory. (For example, functional application corresponds to the familiar classical rule of modus ponens under this view). A number of further axioms give rise to a deductive calculus in which many but not all of the rules deployed by the alternative rule-based generalizations of CG are theorems. For example, the derivation (6) corresponds to a proof in the Lambek calculus using type-raising and composition as lemmas.
The differences between these approaches make themselves felt when the grammars in question are extended beyond the weak context-free power of the Lambek calculus and the combinatory rules that are theorems thereof, as they must be to capture natural language in an explanatory fashion. The problem is that almost any addition of axioms corresponding to the non-Lambek combinatory rules that have been proposed in the rule-based framework causes a collapse of the calculus into "permutation completeness" -- that is, into a grammar that accepts all permutations of the words of any sentence it accepts. This forces the advocates of the Lambek calculus into the "multimodal" systems involving many distinct slashes encoding multiple notions of implication (Morrill 1994), and forces the advocates of rule-based systems to impose type restrictions on their rules. (Nevertheless, Joshi, Vijay-Shanker, and Weir 1991 show that certain rule-based CGs remain of low automata-theoretic power.)
These two styles of CG are reviewed and compared at length by Moortgat (1988) (with a deductive bias), and Wood (1993) (with a rule-based bias) (see Further Readings). To some extent the same biases are respectively exhibited in the selection made in two important collections of papers edited by Buszkowski, Marciszewiski, and van Benthem (1988) and Oehrle, Bach, and Wheeler (1988) (see Further Readings), which include several of the papers cited here.
The differences are less important for the present purpose than the fact that all of these theories have the effect of engendering derivational structures that are much freer than traditional surface structures, while nonetheless guaranteeing that the nonstandard derivations deliver the same semantic interpretation as the standard ones. For example, because all of these theories allow the residue of relativization Dexter thinks that Warren likes in example (6) to be a derivational constituent of type S/NP, they also all allow a nonstandard analysis of the canonical sentence Dexter thinks that Warren likes these flowers in terms of an identically derived constituent followed by an object NP:
This is a surprising property, because it seems to flout all received opinion concerning the surface constituency of English sentences, suggesting that a structure in which objects -- even embedded ones -- dominate subjects is as valid as the standard one in which subjects dominate objects. The implication is that the BINDING THEORY (which must explain such facts as that in every language in the world you can say the equivalent of Warren and Dexter shave each other but not Each other shave Dexter and Warren) must be regarded as a property of semantic interpretation or LOGICAL FORM rather than of surface structure as such (cf. Dowty 1979; Szabolcsi 1989; Chierchia 1988; Hepple 1990; Jacobson 1992).
These proposals also imply that there are many semantically equivalent surface derivations for every traditional one, a problem that is sometimes misleadingly referred to as "spurious ambiguity," and which appears to make parsing more laborious. However, this problem can be eliminated using standard chart-parsing techniques with an equivalence check on Logical Forms associated with constituents, as proposed by Karttunen (1989) and other advocates of unification-based computational realizations of CG -- see Carpenter 1997 for a review.
Flexible or combinatory Categorial Grammars of all kinds have real advantages for capturing a number of phenomena that are problematic for more traditional theories of grammar. For example, as soon as the analysis in (7) is admitted, we explain why similar fragments can behave like constituents for purposes of coordination:
(Other even more spectacular coordinating nonstandard fragments are discussed in Dowty 1988.)
We also explain why intonation seems similarly able to treat such fragments as phrasal units in examples like the following, in which % marks an intonational boundary or break, and capitalization indicates STRESS (cf. Oehrle et al. 1985; Prevost 1995):
Moreover, the availability of semantic interpretations for such nonstandard constituents appears under certain plausible assumptions about the relation of the competence grammar to the processor to simplify the problem of explaining the availability to human sentence processors of semantic interpretations for fragments like the flowers sent for, as evidenced by the effect of this content in (b) below in eliminating the "garden-path" effect of the ambiguity in (a), discussed by Crain and Steedman (1985) and Altman (1988).
All of these phenomena imply that the extra structural ambiguity engendered by generalized categorial grammars is not "spurious," but a property of competence grammar itself.
Ajdukiewicz, K. (1935). Die syntaktische Konnexitat. In S. McCall, Ed., Polish Logic 1920-1939. Oxford University Press, pp. 207 - 231. Translated from Studia Philosophica 1: 1 - 27.
Altmann, G. (1988). Ambiguity, parsing strategies, and computational models. Language and Cognitive Processes 3:73-98.
Bach, E. (1976). An extension of classical transformational grammar. In Problems in Linguistic Metatheory: Proceedings of the 1976 Conference at Michigan State University 183-224.
Bar-Hillel, Y. (1953). A quasi-arithmetical notation for syntactic description. Language 29:47-58.
Carpenter, R. (1997). Type-Logical Semantics. Cambridge, MA: MIT Press.
Chierchia, G. (1988). Aspects of a categorial theory of binding. In R. T. Oehrle, E. Bach, and D. Wheeler, Eds., Categorial Grammars and Natural Language Structures. (Proceedings of the Conference on Categorial Grammar, Tucson, AZ, June 1985.) Dordrecht: Reidel, pp. 153-98.
Chomsky, N. (1957). Syntactic Structures. The Hague: Mouton.
Crain, S., and M. Steedman. (1985). On not being led up the garden path: the use of context by the psychological parser. In L. Kartunnen, D. Dowty, and A. Zwicky, Eds., Natural Language Parsing: Psychological, Computational and Theoretical Perspectives. ACL Studies in Natural Language Processing. Cambridge: Cambridge University Press, pp. 320-358.
Dowty, D. (1979). Dative movement and Thomason's extensions of Montague Grammar. In S. Davis and M. Mithun, Eds., Linguistics, Philosophy, and Montague Grammar. Austin: University of Texas Press.
Dowty, D. (1988). Type-raising, functional composition, and non-constituent coordination. In R. T. Oehrle, E. Bach, and D. Wheeler, Eds., Categorial Grammars and Natural Language Structures. Proceedings of the Conference on Categorial Grammar, Tucson, AZ, June 1985. Dordrecht: Reidel, pp. 153-198.
Geach, P. (1972). A program for syntax. In D. Davidson and G. Harman, Eds., Semantics of Natural Language. Dordrecht: Reidel, pp. 483-497.
Hepple, M. (1990). The Grammar and Processing of Order and Dependency: A Categorial Aproach. Ph.D. diss., University of Edinburgh.
Jacobson, P. (1992). The lexical entailment theory of control and the tough construction. In I. Sag and A. Szabolcsi, Eds., Lexical Matters. Chicago: CSLI/Chicago University Press, pp. 269-300.
Joshi, A., K. Vijay-Shanker, and D. Weir. (1991). The convergence of mildly context-sensitive formalisms. In P. Sells, S. Shieber, and T. Wasow, Eds., Processing of Linguistic Structure. Cambridge MA: MIT Press, pp. 31-81.
Karttunen, L. (1989). Radical lexicalism. In M. R. Baltin and A. S. Kroch, Eds., Alternative Conceptions of Phrase Structure. Chicago: University of Chicago Press.
Lambek, J. (1958). The mathematics of sentence structure. American Mathematical Monthly 65:154-170.
Lewis, D. (1970). General semantics. Synthese 22:18-67.
Lyons, J. (1968). Introduction to Theoretical Linguistics. Cambridge: Cambridge University Press.
Montague, R. (1974). Formal philosophy: Papers of Richard Montague, Richmond H. Thomason, Ed. New Haven: Yale University Press.
Moortgat, M. (1988). Categorial Investigations. Ph.D. diss., Universiteit van Amsterdam. (Published by Foris, 1989).
Morrill, G. (1994). Type-Logical Grammar. Dordrecht: Kluwer.
Oehrle, R. T. (1988). Multidimensional compositional functions as a basis for grammatical analysis. In R. T. Oehrle, E. Bach, and D. Wheeler, Eds., Categorial Grammars and Natural Language Structures. (Proceedings of the Conference on Categorial Grammar, Tucson, AZ, June 1985). Dordrecht: Reidel, pp. 349-390.
Prevost, S. (1995). A Semantics of Contrast and Information Structure for Specifying Intonation in Spoken Language Generation. Ph.D. diss., University of Pennsylvania, Philadelphia, PA.
Szabolcsi, A. (1989). Bound variables in syntax: are there any? In R. Bartsch, J. van Benthem, and P. van Emde Boas, Eds., Semantics and Contextual Expression. Dordrecht: Foris, pp. 295-318.
van Benthem, J. (1986). Essays in Logical Semantics. Dordrecht: Reidel.
Buszkowski, W., W. Marciszewski, and J. van Benthem, Eds. (1988). Categorial Grammar. Amsterdam: John Benjamins.
Moortgat, M. (1997). Categorial type logics. In J. van Benthem and A. ter Meulen, Eds., Handbook of Logic and Language. Amsterdam: North Holland, pp. 93-177.
Oehrle, R., E. Bach, and D. Wheeler. (1988). Categorial Grammars and Natural Language Structures. Dordrecht: Reidel.
Steedman, M. (1996). Surface Structure and Interpretation. Linguistic Inquiry Monograph 30. Cambridge MA: MIT Press.
Wood, M. M. (1993). Categorial Grammar. Routledge.