The goal of computational neuroscience is to explain in computational terms how brains generate behaviors. Computational models of the brain explore how populations of highly interconnected neurons are formed during development and how they come to represent, process, store, act on, and be altered by information present in the environment (Churchland and Sejnowski 1992). Techniques from computer science and mathematics are used to simulate and analyze these computational models to provide links between the widely ranging levels of investigation, from the molecular to the systems levels. Only a few key aspects of computational neuroscience are covered here (see Arbib 1995 for a comprehensive handbook of brain theory and neural networks).
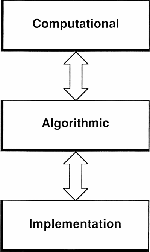
The term computational refers both to the techniques used in computational neuroscience and to the way brains process information. Many different types of physical systems can solve computational problems, including slide rules and optical analog analyzers as well as digital computers, which are analog at the level of transistors and must settle into a stable state on each clock cycle. What these have in common is an underlying correspondence between an abstract computational description of a problem, an algorithm that can solve it, and the states of the physical system that implement it (figure 1). This is a broader approach to COMPUTATION than one based purely on symbol processing.

Figure 1 Levels of analysis (Marr 1982). The two-way arrows indicate that constraints between levels can be used to gain insights in both directions.
There is an important distinction between general-purpose computers, which can be programmed to solve many different types of algorithms, and special-purpose computers, which are designed to solve only a limited range of problems. Most neural systems are specialized for particular tasks, such as the RETINA, which is dedicated to visual transduction and image processing. As a consequence of the close coupling between structure and function in a brain area, anatomy and physiology can provide important clues to the algorithms implemented, and the computational function of that area (figure 1), which might not be apparent in a general-purpose computer whose function depends on software.
Another major difference between the brain and a general-purpose digital computer is that the connectivity between neurons and their properties are shaped by the environment during development and remain plastic even in adulthood. Thus, as the brain processes information, it changes its own structure in response to the information being processed. Adaptation and learning are important mechanisms that allow brains to respond flexibly as the world changes on a wide range of time scales, from seconds to years. The flexibility of the brain has survival advantages when the environment is nonstationary and the evolution of cognitive skills may deeply depend on genetic processes that have extended the time scales for brain plasticity.
Brains are complex, dynamic systems, and brain models provide intuition about the possible behaviors of such systems, especially when they are nonlinear and have feedback loops. The predictions of a model make explicit the consequences of the underlying assumptions, and comparison with experimental results can lead to new insights and discoveries. Emergent properties of neural systems, such as oscillatory behaviors, depend on both the intrinsic properties of the neurons and the pattern of connectivity between them.
Perhaps the most successful model at the level of the NEURON has been the classic Hodgkin- Huxley (1952) model of the action potential in the giant axon of the squid (Koch and Segev 1998). Data were collected under a variety of conditions, and a model later constructed to integrate the data into a unified framework. Because most of the variables in the model are measured experimentally, only a few unknown parameters need to be fit to the experimental data. Detailed models can be used to choose among experiments that could be used to distinguish between different explanations of the data.
The classic model of a neuron, in which information flows from the dendrites, where synaptic signals are integrated, to the soma of the neuron, where action potentials are initiated and carried to other neurons through long axons, views dendrites as passive cables. Recently, however, voltage-dependent sodium, calcium, and potassium channels have been observed in the dendrites of cortical neurons, which greatly increases the complexity of synaptic integration. Experiments and models have shown that these active currents can carry information in a retrograde direction from the cell body back to the distal synapse tree (see also COMPUTING IN SINGLE NEURONS). Thus it is possible for spikes in the soma to affect synaptic plasticity through mechanisms that were suggested by Donald HEBB in 1949.
Realistic models with several thousand cortical neurons can be explored on the current generation of workstation. The first model for the orientation specificity of neurons in the VISUAL CORTEX was the feedforward model proposed by Hubel and Wiesel (1962), which assumed that the orientation preference of cortical cells was determined primarily by converging inputs from thalamic relay neurons. Although solid experimental evidence supports this model, local cortical circuits have been shown to be important in amplifying weak signals and suppressing noise as well as performing gain control to extend the dynamic range. These models are governed by the type of attractor dynamics analyzed by John Hopfield (1982), who provided a conceptual framework for the dynamics of feedback networks (Churchland and Sejnowski 1992).
Although the spike train of cortical neurons is highly irregular, and is typically treated statistically, information may be contained in the timing of the spikes in addition to the average firing rate. This has already been established for a variety of sensory systems in invertebrates and for peripheral sensory systems in mammals (Rieke et al. 1996). Whether spike timing carries information in cortical neurons remains, however, an open research issue (Ritz and Sejnowski 1997). In addition to representing information, spike timing could also be used to control synaptic plasticity through Hebbian mechanisms for synaptic plasticity.
Other models have been used to analyze experimental data in order to determine whether they are consistent with a particular computational assumption. For example, Apostolos Georgopoulos has used a "vector-averaging" technique to compute the direction of arm motion from the responses of cortical neurons, and William Newsome and his colleagues (Newsome, Britten, and Movshon 1989) have used SIGNAL DETECTION THEORY to analyze the information from cortical neurons responding to visual motion stimuli (Churchland and Sejnowski 1992). In these examples, the computational model was used to explore the information in the data but was not meant to be a model for the actual cortical mechanisms. Nonetheless, these models have been highly influential and have provided new ideas for how the cortex may represent sensory information and motor commands.
A NEURAL NETWORK model that simplifies the intrinsic properties of neurons can help us understand the information contained in populations of neurons and the computational consequences. An example of this approach is a recent model of parietal cortex (Pouget and Sejnowski 1997) based on the response properties of cortical neurons, which are involved in representing spatial location of objects in the environment. Examining which reference frames are used in the cortex for performing sensorimotor transformations, the model makes predictions for experiments performed on patients with lesions of the parietal cortex who display spatial neglect.
Conceptual models can be helpful in organizing experimental facts. Although thalamic neurons that project to the cortex are called "relay cells," they almost surely have additional functions because the visual cortex makes massive feedback projections back to them. Francis Crick (1994) has proposed that the relay cells in the THALAMUS may be involved in ATTENTION, and has provided an explanation for how this could be accomplished based on the anatomy of the thalamus. His searchlight model of attention and other hypotheses for the function of the thalamus are being explored with computational models and new experimental techniques. Detailed models of thalamocortical networks can already reproduce the low-frequency oscillations observed during SLEEP states, when feedback connections to the thalamus affect the spatial organization of the rhythms. These sleep rhythms may be important for memory consolidation (Sejnowski 1995).
Finally, small neural systems have been analyzed with dynamic systems theory. This approach is feasible when the numbers of parameters and variables are small. Most models of neural networks involve a large number of variables, such as membrane potentials, firing rates, and concentrations of ions, with an even greater number of unknown parameters, such as synaptic strengths, rate constants, and ionic conductances. In the limit that the number of neurons and parameters is very large, techniques from statistical physics can be applied to predict the average behavior of large systems. There is a midrange of systems where neither type of limiting analysis is possible, but where simulations can be performed. One danger of relying solely on computer simulations is that they may be as complex and difficult to interpret as the biological systems themselves.
To better understand the higher cognitive functions, we will need to scale up simulations from thousands to millions of neurons. While parallel computers are available that permit massively parallel simulations, the difficulty of programming these computers has limited their usefulness. A new approach to massively parallel models has been introduced by Carver Mead (1989), who builds subthreshold complementary metal-oxide semiconductor Very-Large-Scale Integrated (CMOS VLSI) circuits with components that directly mimic the analog computational operations in neurons. Several large silicon chips have been built that mimic the visual processing found in retinas. Analog VLSI cochleas have also been built that can analyze sound in real time. These chips use analog voltages and currents to represent the signals, and are extremely efficient in their use of power compared to digital VLSI chips. A new branch of engineering called "neuromorphic engineering" has arisen to exploit this technology.
Recently, analog VLSI chips have been designed and built that mimic the detailed biophysical properties of neurons, including dendritic processing and synaptic conductances (Douglas, Mahowald, and Mead 1995), which has opened the possibility of building a "silicon cortex." Protocols are being designed for long-distance communication between analog VLSI chips using the equivalent of all-or-none spikes, to mimic long-distance communication between neurons.
Many of the design issues that govern the evolution of biological systems also arise in neuromorphic systems, such as the trade-off in cost between short-range connections and expensive long-range communication. Computational models that quantify this trade-off and apply a minimization procedure can predict the overall organization of topographical maps and columnar organization of the CEREBRAL CORTEX.
Although brain models are now routinely used as tools for interpreting data and generating hypotheses, we are still a long way from having explanatory theories of brain function. For example, despite the relatively stereotyped anatomical structure of the CEREBELLUM, we still do not understand its computational functions. Recent evidence from functional imaging of the cerebellum suggests that it is involved in higher cognitive functions, and not just a motor controller. Modeling studies may help to sort out competing hypotheses. This has already occurred in the oculomotor system, which has a long tradition of using control theory models to guide experimental studies.
Computational neuroscience is a relatively young, rapidly growing discipline. Although we can now simulate only small parts of neural systems, as digital computers continue to increase in speed, it should become possible to approach more complex problems. Most of the models developed thus far have been aimed at interpreting experimental data and providing a conceptual framework for the dynamic properties of neural systems. A more comprehensive theory of brain function should arise as we gain a broader understanding of the computational resources of nervous systems at all levels of organization.
Arbib, A. M. (1995). The Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press.
Churchland P. S., and T. J. Sejnowski. (1992). The Computational Brain. Cambridge, MA: MIT Press.
Crick, F. H. C. (1994). The Astonishing Hypothesis: The Scientific Search for the Soul. New York: Scribner.
Douglas R., M. Mahowald, and C. Mead. (1995). Neuromorphic analogue VLSI . Annual Review of Neuroscience 18:255-281.
Hebb, D. O. (1949). Organization of Behavior. New York: Wiley.
Hodgkin, A. L., and A. F. Huxley. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500-544.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA 79:2554-2558.
Hubel, D., and T. Wiesel. (1962). Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. Journal of Physiology 160:106-154.
Koch, C., and I. Segev. (1998). Methods in Neuronal Modeling: From Synapses to Networks. Second edition. Cambridge, MA: MIT Press.
Marr, D. (1982). Vision. San Francisco: Freeman.
Mead, C., and M. Ismail, Eds. (1989). Analog VLSI implementation of neural systems. Boston: Kluwer Academic Publishers.
Newsome, W. T., K. H. Britten, and J. A. Movshon. (1989). Neuronal correlates of a perceptual decision. Nature 341:52-54
Pouget, A., and T. J. Sejnowski. (1997). A new view of hemineglect based on the response properties of parietal neurons. Philosophical Transactions of the Royal Society 352:1449-1459.
Rieke, F., D. Warland, R. de Ruyter van Steveninck, and W. Bialek. (1996). Spikes: Exploring the Neural Code. Cambridge, MA: MIT Press.
Ritz, R., and T. J. Sejnowski. (1997). Synchronous oscillatory activity in sensory systems: New vistas on mechanisms. Current Opinion in Neurobiology 7:536-546.
Sejnowski, T. J. (1995). Sleep and memory. Current Biology 5:832-834.