Modal Logic
In classical
propositional LOGIC all the operators are truth-functional. That
is to say, the truth or falsity of a complex formula depends only on
the truth or falsity of its simpler propositional constituents.
Modal logic is concerned to understand propositions about what must or might be the
case. We might, for example, have two propositions alike in truth
value, both true say, where one is true and could not possibly be
false, while the other is true but might easily have been false.
Thus it must be that 2 + 2 = 4, but while
it is true that I am writing this entry, it might easily not have
been. Modal logic extends the well-formed formulas (wff) of classical
logic by the addition of a one-place sentential operator L (or  ), interpreted as meaning "It
is necessary that." Using this operator, a one-place operator M (or
), interpreted as meaning "It
is necessary that." Using this operator, a one-place operator M (or
 ) meaning "It is possible
that" may be defined as ~L~, where ~ is a (classical)
negation operator, and a two-place operator
) meaning "It is possible
that" may be defined as ~L~, where ~ is a (classical)
negation operator, and a two-place operator
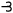 meaning "entails" may be defined as
meaning "entails" may be defined as
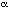
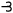 =
= 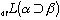 ,
where
,
where 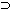 is
classical material implication. In fact, any one of L, M,
or
is
classical material implication. In fact, any one of L, M,
or 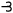 can
be taken as primitive, and the others defined in terms of it.
can
be taken as primitive, and the others defined in terms of it.
Although Lp is usually read
as "Necessarily p," it need not be restricted
to a single narrowly conceived sense of "necessarily." Very
often, for example, when we say that something must be
so, we can be taken to be claiming that it is so; and if
we take L to express "must be" in this
sense, we shall want to have it as a principle that whenever Lp is
true, so is p itself. A system of logic that expresses
this idea will have Lp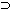 p as
one of its valid formulas. On the other hand, there are uses of
words such as "must" and "necessary" that
express not what necessarily is so but rather what ought
to be so, and if we interpret L in accordance with
these uses, we shall want to allow the possibility that Lp may
be true but p itself false because people do not always
do what they ought to do. And fruitful systems of logic have been
inspired by the idea of taking the necessity operator to mean, for
example, "It will always be the case that," "It
is known that," or "It is provable that." In
fact, one of the important features of modal logic is that out of
the same basic material can be constructed a variety of systems that
reflect a variety of interpretations of L, within a range
that can be indicated, somewhat loosely, by calling L a "necessity
operator."
p as
one of its valid formulas. On the other hand, there are uses of
words such as "must" and "necessary" that
express not what necessarily is so but rather what ought
to be so, and if we interpret L in accordance with
these uses, we shall want to allow the possibility that Lp may
be true but p itself false because people do not always
do what they ought to do. And fruitful systems of logic have been
inspired by the idea of taking the necessity operator to mean, for
example, "It will always be the case that," "It
is known that," or "It is provable that." In
fact, one of the important features of modal logic is that out of
the same basic material can be constructed a variety of systems that
reflect a variety of interpretations of L, within a range
that can be indicated, somewhat loosely, by calling L a "necessity
operator."
In the early days of modal logic, disputes centered round the question
of whether a given principle of modal logic was correct. Typically,
these disputes involved formulas in which one modal operator occurs
within the scope of another -- formulas such as Lp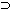 LLp. Is a necessary proposition
necessarily necessary? A number of different modal systems were
produced that reflected different views about which principles were
correct. Until the early sixties, however, modal logics were discussed
almost exclusively as axiomatic systems without access to a notion of
validity of the kind used, for example, in the truth table method for
determining the validity of wff of the classical propositional
calculus. The semantical breakthrough came by using the idea that a
necessary proposition is one true in all possible worlds. But whether
another world counts as possible may be held to be relative to the
world of origin. Thus an interpretation or model for a modal
system would consist of a set W of possible worlds and a relation R of
accessibility between them. For any wff
LLp. Is a necessary proposition
necessarily necessary? A number of different modal systems were
produced that reflected different views about which principles were
correct. Until the early sixties, however, modal logics were discussed
almost exclusively as axiomatic systems without access to a notion of
validity of the kind used, for example, in the truth table method for
determining the validity of wff of the classical propositional
calculus. The semantical breakthrough came by using the idea that a
necessary proposition is one true in all possible worlds. But whether
another world counts as possible may be held to be relative to the
world of origin. Thus an interpretation or model for a modal
system would consist of a set W of possible worlds and a relation R of
accessibility between them. For any wff 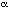 and world w, L
and world w, L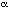 will be true at w iff
will be true at w iff 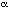 itself is true at every w ' such
that wRw'. It can then happen that whether a
principle of modal logic holds can depend on properties of the
accessibility relation. Suppose that R is required to be transitive,
that is, suppose that, for any worlds w1,
w2, and w3, if
w1Rw 2 and
w2Rw3, then w
1Rw3. If so, then Lp
itself is true at every w ' such
that wRw'. It can then happen that whether a
principle of modal logic holds can depend on properties of the
accessibility relation. Suppose that R is required to be transitive,
that is, suppose that, for any worlds w1,
w2, and w3, if
w1Rw 2 and
w2Rw3, then w
1Rw3. If so, then Lp 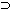 LLp will be valid, but if
nontransitive models are permitted, it need not be. If R is reflexive,
that is, if wRw for every world w, then
Lp
LLp will be valid, but if
nontransitive models are permitted, it need not be. If R is reflexive,
that is, if wRw for every world w, then
Lp 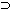 p is valid. Thus
different systems of modal logic can represent different ways of
restricting necessity.
p is valid. Thus
different systems of modal logic can represent different ways of
restricting necessity.
It is possible to extend modal logic by having logics that involve
more than one modal operator. One particularly important class of
multimodal systems is the class of tense logics. A tense
logic has two operators, L 1 and
L2, where L1 means "it always
will be the case that" and L2 means "it always has
been the case that". (In a tense logic L1 and
L2 are often written G and H,
with their possibility versions as P for ~H~, and
F for ~G~.) More elaborate families of modal
operators are suggested by possible interpretations of modal logic in
computer science. In these interpretations the "worlds" are states in
the running of a program. If 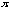 is a
computer program, then [
is a
computer program, then [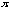 ]
]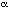 means that after program
means that after program 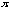 has been run, a will be true. If w is
any "world," then wR
has been run, a will be true. If w is
any "world," then wR 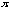 w' means that state w'
results from the running of program
w' means that state w'
results from the running of program 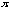 . This
extension of modal logic is called "dynamic logic."
. This
extension of modal logic is called "dynamic logic."
First-order predicate logic can also
be extended by the addition of modal operators. The most interesting
consequences of such extensions are those which affect "mixed" principles, principles
that relate quantifiers and modal operators and that cannot be stated
at the level of modal propositional logic or nonmodal predicate
logic. Thus where 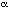 is any wff,
is any wff,
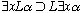 is valid, but for some wff
is valid, but for some wff
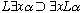 need not be. (Even
if a game must have a winner, there need be no one who must win.)
In some cases the principles of the extended system will depend
on the propositional logic on which it is based. An example is the
schema
need not be. (Even
if a game must have a winner, there need be no one who must win.)
In some cases the principles of the extended system will depend
on the propositional logic on which it is based. An example is the
schema
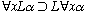 (often known as the "Barcan formula"), which is provable
in some modal systems but not in others. If both directions are
assumed, so that we have
(often known as the "Barcan formula"), which is provable
in some modal systems but not in others. If both directions are
assumed, so that we have
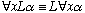 ,
then this formula expresses the principle that the domain of individuals
is held constant as we move from one world to another accessible world.
,
then this formula expresses the principle that the domain of individuals
is held constant as we move from one world to another accessible world.
When identity is added, even more
questions arise. The usual axioms for identity easily allow the
derivation of (x = y) 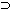 L(x = y),
but should we really say that all identities are necessary? Questions
like this bring us to the boundary between modal logic and metaphysics
and remind us of the rich potential that the theory of possible
worlds has for illuminating such issues. POSSIBLE WORLDS SEMANTICS can be generalized to deal with any operators
whose meanings are operations on propositions as sets of possible
worlds, and form a congenial tool for those who think that the meaning
of a sentence is its truth conditions, and that these should be
taken literally as a set of possible worlds -- the worlds
in which the sentence is true. Such generalizations give rise to
fruitful tools in providing a framework for semantical theories
for natural languages.
L(x = y),
but should we really say that all identities are necessary? Questions
like this bring us to the boundary between modal logic and metaphysics
and remind us of the rich potential that the theory of possible
worlds has for illuminating such issues. POSSIBLE WORLDS SEMANTICS can be generalized to deal with any operators
whose meanings are operations on propositions as sets of possible
worlds, and form a congenial tool for those who think that the meaning
of a sentence is its truth conditions, and that these should be
taken literally as a set of possible worlds -- the worlds
in which the sentence is true. Such generalizations give rise to
fruitful tools in providing a framework for semantical theories
for natural languages.
See also
Additional links
-- Max Cresswell
Further Readings
Chellas, B. F. (1980). Modal Logic: An
Introduction. Cambridge: Cambridge University Press.
Hughes, G. E., and M. J. Cresswell. (1996). A
New Introduction to
Modal Logic. London: Routledge.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
 ), interpreted as meaning "It
is necessary that." Using this operator, a one-place operator M (or
), interpreted as meaning "It
is necessary that." Using this operator, a one-place operator M (or
 ) meaning "It is possible
that" may be defined as ~L~, where ~ is a (classical)
negation operator, and a two-place operator
) meaning "It is possible
that" may be defined as ~L~, where ~ is a (classical)
negation operator, and a two-place operator
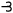 meaning "entails" may be defined as
meaning "entails" may be defined as
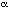
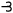 =
= 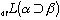 ,
where
,
where 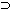 is
classical material implication. In fact, any one of L, M,
or
is
classical material implication. In fact, any one of L, M,
or 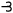 can
be taken as primitive, and the others defined in terms of it.
can
be taken as primitive, and the others defined in terms of it.
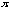 is a
computer program, then [
is a
computer program, then [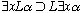 is valid, but for some wff
is valid, but for some wff
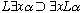 need not be. (Even
if a game must have a winner, there need be no one who must win.)
In some cases the principles of the extended system will depend
on the propositional logic on which it is based. An example is the
schema
need not be. (Even
if a game must have a winner, there need be no one who must win.)
In some cases the principles of the extended system will depend
on the propositional logic on which it is based. An example is the
schema
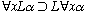 (often known as the "Barcan formula"), which is provable
in some modal systems but not in others. If both directions are
assumed, so that we have
(often known as the "Barcan formula"), which is provable
in some modal systems but not in others. If both directions are
assumed, so that we have
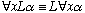 ,
then this formula expresses the principle that the domain of individuals
is held constant as we move from one world to another accessible world.
,
then this formula expresses the principle that the domain of individuals
is held constant as we move from one world to another accessible world.