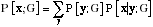
Equation 1
Unsupervised learning studies how systems can learn to represent particular input patterns in a way that reflects the statistical structure of the overall collection of input patterns. By contrast with SUPERVISED LEARNING or REINFORCEMENT LEARNING, there are no explicit target outputs or environmental evaluations associated with each input; rather, the unsupervised learner brings to bear prior biases as to what aspects of the structure of the input should be captured in the output.
Unsupervised learning is important because it is likely to be much more common in the brain than supervised learning. For instance there are around 108 photoreceptors in each eye whose activities are constantly changing with the visual world and which provide all the information that is available to indicate what objects there are in the world, how they are presented, what the lighting conditions are, and so forth. Developmental and adult plasticity are critical in animal vision (see VISION AND LEARNING) -- indeed, structural and physiological properties of synapses in the neocortex are known to be substantially influenced by the patterns of activity in sensory neurons that occur. However, essentially none of the information about the contents of scenes is available during learning. This makes unsupervised methods essential, and, equally, allows them to be used as computational models for synaptic adaptation.
The only things that unsupervised learning methods have to work with are the observed input patterns x which are often assumed to be independent samples from an underlying unknown probability distribution PI[x], and some explicit or implicit a priori information as to what is important. One key notion is that input, such as the image of a scene, has distal independent causes, such as objects at given locations illuminated by particular lighting. Because it is on those independent causes that we normally must act, the best representation for an input is in their terms. Two classes of method have been suggested for unsupervised learning. Density estimation techniques explicitly build statistical models (such as BAYESIAN NETWORKS) of how underlying causes could create the input. Feature extraction techniques try to extract statistical regularities (or sometimes irregularities) directly from the inputs.
Unsupervised learning in general has a long and distinguished history. Some early influences were Horace Barlow (see Barlow 1989), who sought ways of characterizing neural codes; Donald MacKay (1956), who adopted a cybernetic- theoretic approach; and David MARR (1970), who made an early unsupervised learning postulate about the goal of learning in his model of the neocortex. The Hebb rule (HEBB 1949), which links statistical methods to neurophysiological experiments on plasticity, has also cast a long shadow. Geoffrey Hinton and Terrence Sejnowski, in inventing a model of learning called the Boltzmann machine (1986), imported many of the concepts from statistics that now dominate the density estimation methods (Grenander 1976-1981). Feature extraction methods have generally been less extensively explored.
Clustering provides a convenient example. Consider the case in which the inputs are the photoreceptor activities created by various images of an apple or an orange. In the space of all possible activities, these particular inputs form two clusters, with many fewer degrees of variation than 108, that is, lower dimension. One natural task for unsupervised learning is to find and characterize these separate, low dimensional clusters.
The larger class of unsupervised learning methods consists of maximum likelihood (ML) density estimation methods. All of these are based on building parameterized models P [x;G] (with parameters G) of the probability distribution PI[x], where the forms of the models (and possibly prior distributions over the parameters G) are constrained by a priori information in the form of the representational goals. These are called synthetic or generative models, because, given a particular value of G, they specify how to synthesize or generate samples x from P [x; G], whose statistics should match PI[x]. A typical model has the structure:
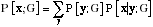
where y represents all the potential causes of the input x. The typical measure of the degree of mismatch is called the Kullback-Leibler divergence:
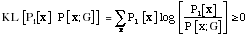
with equality if and only if PI[x] = P [x; G].
Given an input pattern x, the most general output of this model is the posterior, analytical, or recognition distribution P [y | x; G], which recognizes which particular causes might underlie x. This analytical distribution is the statistical inverse of the synthetic distribution.
A very simple model can be used in
the example of clustering (Nowlan 1990). Consider the case in which
there are two values for y (1 and 2), with
P [y=1] =
 ;
P [y=2] = 1 -
;
P [y=2] = 1 -  ,
where
,
where  is called a mixing proportion, and two different Gaussian
distributions for the activities x of the photoreceptors
depending on which y is chosen:
is called a mixing proportion, and two different Gaussian
distributions for the activities x of the photoreceptors
depending on which y is chosen:
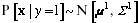 and
and 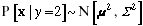 , where
, where 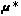 are means and
are means and 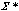 are covariance matrices. Unsupervised learning of the
means determines the locations of centers of the clusters, and of
the mixing proportions and the covariances characterizes the size
and (rather coarsely) the shape of the clusters. The posterior distribution
are covariance matrices. Unsupervised learning of the
means determines the locations of centers of the clusters, and of
the mixing proportions and the covariances characterizes the size
and (rather coarsely) the shape of the clusters. The posterior distribution
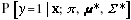 reports
how likely it is that a new image x was generated
from the first cluster, that is, that y=1 is the
true hidden cause. Clustering can occur (with or) without any supervision information
about the different classes. This model is called a mixture
of Gaussians.
reports
how likely it is that a new image x was generated
from the first cluster, that is, that y=1 is the
true hidden cause. Clustering can occur (with or) without any supervision information
about the different classes. This model is called a mixture
of Gaussians.
Maximum likelihood density estimation, and approximations to it, cover a very wide spectrum of the principles that have been suggested for unsupervised learning. This includes versions of the notion that the outputs should convey most of the information in the input; that they should be able to reconstruct the inputs well, perhaps subject to constraints such as being independent or sparse; and that they should report on the underlying causes of the input. Many different mechanisms apart from clustering have been suggested for each of these, including forms of Hebbian learning, the Boltzmann and Helmholtz machines, sparse coding, various other mixture models, and independent components analysis.
Density estimation is just a heuristic
for learning good representations. It can be too stringent -- making
it necessary to build a model of all the irrelevant richness in
sensory input. It can also be too lax -- a look-up table that
reported
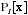 for each x might be an excellent way of modeling the
distribution, but provides no way to represent particular examples x.
for each x might be an excellent way of modeling the
distribution, but provides no way to represent particular examples x.
The smaller class of unsupervised learning methods seeks to discover how to represent the inputs x by defining some quality that good features have, and then searching for those features in the inputs. For instance, consider the case that the output y(x) = w · x is a linear projection of the input onto a weight vector w. The central limit theorem implies that most such linear projections will have Gaussian statistics. Therefore if one can find weights w such that the projection has a highly non-Gaussian (for instance, multimodal) distribution, then the output is likely to reflect some interesting aspect of the input. This is the intuition behind a statistical method called projection pursuit. It has been shown that projection pursuit can be implemented using a modified form of Hebbian learning (Intrator and Cooper 1992). Arranging that different outputs should represent different aspects of the input turns out to be surprisingly tricky.
Projection pursuit can also execute a form of clustering in the example. Consider projecting the photoreceptor activities onto the line joining the centers of the clusters. The distribution of all activities will be bimodal -- one mode for each cluster -- and therefore highly non-Gaussian. Note that this single projection does not itself characterize well the nature or shape of the clusters.
Another example of a heuristic underlying good features is that causes are often somewhat global. For instance, consider the visual input from an object observed in depth. Different parts of the object may share few features, except that they are at the same depth, that is, one aspect of the disparity in the information from the two eyes at the separate locations is similar. This is the global underlying feature. By maximizing the mutual information between different outputs that are calculated on the basis of the separate input, one can find this disparity. This technique was invented by Becker and Hinton (1992) and is called IMAX.
Barlow, H. B. (1989). Unsupervised learning. Neural Computation 1:295-311.
Becker, S., and G. E. Hinton. (1992). A self-organizing neural network that discovers surfaces in random-dot stereograms. Nature 355:161-163.
Grenander, U. (1976-1981). Lectures in Pattern Theory 1, 2, and 3: Pattern Analysis, Pattern Synthesis and Regular Structures. Berlin: Springer.
Hebb, D. O. (1949) The Organization of Behavior. New York: Wiley.
Hinton, G. E., and T. J. Sejnowski. (1986). Learning and relearning in Boltzmann machines. In D. E. Rumelhart, J. L. McClelland, and the PDP Research Group, Eds., Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Vol. 1, Foundations. Cambridge, MA: MIT Press, pp. 282-317.
Intrator, N., and L. N. Cooper. (1992). Objective function formulation of the BCM theory of visual cortical plasticity: Statistical connections, stability conditions. Neural Networks 5:3-17.
MacKay, D. M. (1956). The epistemological problem for automata. In C. E. Shannon and J. McCarthy, Eds., Automata Studies. Princeton, NJ: Princeton University Press, pp. 235-251.
Marr, D. (1970). A theory for cerebral neocortex. Proceedings of the Royal Society of London, Series B 176:161-234.
Nowlan, S. J. (1990). Maximum likelihood competitive learning. In D. S. Touretzky, Ed., Advances in Neural Information Processing Systems, 2. San Mateo, CA: Kaufmann.
Becker, S., and M. Plumbley. (1996). Unsupervised neural network learning procedures for feature extraction and classification. International Journal of Applied Intelligence 6:185-203.
Dayan, P., G. E. Hinton, R. M. Neal, and R. S. Zemel. (1995). The Helmholtz machine. Neural Computation 7:889-904.
Hinton, G. E. (1989). Connectionist learning procedures. Artificial Intelligence 40:185-234.
Linsker, R. (1988). Self-organization in a perceptual network. Computer 21:105-128.
Mumford, D. (1994). Neuronal architectures for pattern-theoretic problems. In C. Koch and J. Davis, Eds., Large-Scale Theories of the Cortex. Cambridge, MA: MIT Press, pp. 125-152.
Olshausen, B. A., and D. J. Field. (1996). Emergence of simple-cell receptive field properties by learning a sparse code for nat ural images. Nature 381:607-609.