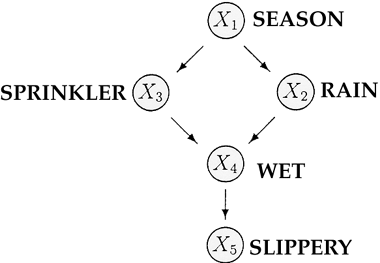
Figure 1 A Bayesian network representing causal influences among five variables.
Bayesian networks were conceptualized in the late 1970s to model distributed processing in READING comprehension, where both semantical expectations and perceptual evidence must be combined to form a coherent interpretation. The ability to coordinate bidirectional inferences filled a void in EXPERT SYSTEMS technology of the early 1980s, and Bayesian networks have emerged as a general representation scheme for uncertain knowledge (Pearl 1988; Shafer and Pearl 1990; Heckerman, Mamdani, and Wellman 1995; Jensen 1996; Castillo, Gutierrez, and Hadi 1997).
Bayesian networks are directed acyclic graphs (DAGs) in which the nodes represent variables of interest (e.g., the temperature of a device, the gender of a patient, a feature of an object, the occurrence of an event) and the links represent informational or causal dependencies among the variables. The strength of a dependency is represented by conditional probabilities that are attached to each cluster of parent-child nodes in the network.
Figure 1 describes a simple yet typical Bayesian network: the causal relationships between the season of the year (X1), whether rain falls (X2) during the season, whether the sprinkler is on (X3) during that season, whether the pavement would get wet (X4), and whether the pavement would be slippery (X5). Here the absence of a direct link between X1 and X 5, for example, captures our understanding that the influence of seasonal variations on the slipperiness of the pavement is mediated by other conditions (e.g., wetness).

Figure 1 A Bayesian network representing causal influences among five variables.
As this example illustrates, a Bayesian network constitutes a model of the environment rather than, as in many other KNOWLEDGE REPRESENTATION schemes (e.g., rule-based systems and NEURAL NETWORKS), a model of the reasoning process. It simulates, in fact, the mechanisms that operate in the environment, and thus facilitates diverse modes of reasoning, including prediction, abduction, and control.
Prediction and abduction require an economical representation of a joint distribution over the variables involved. Bayesian networks achieve such economy by specifying, for each variable Xi, the conditional probabilities P(xi | pai) where pai is a set of predecessors (of Xi) that render Xi independent of all its other predecessors. Variables judged to be the direct causes of Xi satisfy this property, and these are depicted as the parents of Xi in the graph. Given this specification, the joint distribution is given by the product
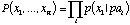
Equation 1
from which all probabilistic queries (e.g., Find the most likely explanation for the evidence) can be answered coherently using probability calculus.
The first algorithms proposed for probabilistic calculations in Bayesian networks used message-passing architecture and were limited to trees (Pearl 1982; Kim and Pearl 1983). Each variable was assigned a simple processor and permitted to pass messages asynchronously with its neighbors until equilibrium was achieved. Techniques have since been developed to extend this tree propagation method to general networks. Among the most popular are Lauritzen and Spiegelhalter's (1988) method of join-tree propagation, and the method of cycle-cutset conditioning (see Pearl 1988, 204-210; Jensen 1996).
While inference in general networks is NP-hard, the computational complexity for each of the methods cited above can be estimated prior to actual processing. When the estimates exceed reasonable bounds, an approximation method such as stochastic simulation (Pearl 1987; 1988, 210-223) can be used instead. Learning techniques have also been developed for systematically updating the conditional probabilities P(xi | pa i) and the structure of the network, so as to match empirical data (see Spiegelhalter and Lauritzen 1990; Cooper and Herskovits 1990).
The most distinctive feature of Bayesian networks, stemming largely from their causal organization, is their ability to represent and respond to changing configurations. Any local reconfiguration of the mechanisms in the environment can be translated, with only minor modification, into an isomorphic reconfiguration of the network topology. For example, to represent a disabled sprinkler, we simply delete from the network all links incident to the node "Sprinkler." To represent the policy of turning the sprinkler off when it rains, we simply add a link between "Rain" and "Sprinkler" and revise P(x3 | x1, x2). This flexibility is often cited as the ingredient that marks the division between deliberative and reactive agents, and that enables deliberative agents to manage novel situations instantaneously, without requiring retraining or adaptation.
Organizing one's knowledge around stable causal mechanisms provides a basis for planning under UNCERTAINTY (Pearl 1996). Once we know the identity of the mechanism altered by the intervention and the nature of the alteration, the overall effect of an intervention can be predicted by modifying the corresponding factors in equation 1 and using the modified product to compute a new probability function. For example, to represent the action "turning the sprinkler ON" in the network of figure 1, we delete the link X1 → X3 and fix the value of X3 to ON. The resulting joint distribution on the remaining variables will be
P(x1, x2, x3, x4, x5) = P(x1) P(x1 | x2) P(x4 | x2, X3 = ON) P(x5 | x4)
Equation 2
Note the difference between the observation X3 = ON, encoded by ordinary Bayesian conditioning, and the action do(X3 = ON), encoded by conditioning a mutilated graph, with the link X1 → X3 removed. This indeed mirrors the difference between seeing and doing: after observing that the sprinkler is ON, we wish to infer that the season is dry, that it probably did not rain, and so on; no such inferences should be drawn in evaluating the effects the contemplated action "turning the sprinkler ON."
One of the most exciting prospects in recent years has been the possibility of using Bayesian networks to discover causal structures in raw statistical data (Pearl and Verma 1991; Spirtes, Glymour, and Schienes 1993). Although any inference from association to CAUSATION is bound to be less reliable than one based on controlled experiment, we can still guarantee an aspect of reliability called "stability": Any alternative structure compatible with the data must be less stable than the structure inferred, which is to say, slight fluctuations in parameters will render that structure incompatible with the data. With this form of guarantee, the theory provides criteria for identifying genuine and spurious causes, with or without temporal information, and yields algorithms for recovering causal structures with hidden variables from empirical data.
In mundane decision making, beliefs are revised not by adjusting numerical probabilities but by tentatively accepting some sentences as "true for all practical purposes." Such sentences, called "plain beliefs," exhibit both logical and probabilistic character. As in classical LOGIC, they are propositional and deductively closed; as in probability, they are subject to retraction and to varying degrees of entrenchment. Bayesian networks can be adopted to model the dynamics of plain beliefs by replacing ordinary probabilities with nonstandard probabilities, that is, probabilities that are infinitesimally close to either zero or one (Goldszmidt and Pearl 1996).
Although Bayesian networks can model a wide spectrum of cognitive activity, their greatest strength is in CAUSAL REASONING, which in turn facilitates reasoning about actions, explanations, counterfactuals, and preferences. Such capabilities are not easily implemented in neural networks, whose strengths lie in quick adaptation of simple motor-visual functions.
Some questions arise: Does an architecture resembling that of Bayesian networks exist anywhere in the human brain? If not, how does the brain perform those cognitive functions at which Bayesian networks excel? A plausible answer to the second question is that fragmented structures of causal organizations are constantly being assembled on the fly, as needed, from a stock of functional building blocks. For example, the network of figure 1 may be assembled from several neural networks, one specializing in the experience surrounding seasons and rains, another in the properties of wet pavements, and so forth. Such specialized networks are probably stored permanently in some mental library, from which they are drawn and assembled into the structure shown in figure 1 only when a specific problem presents itself, for example, to determine whether an operating sprinkler could explain why a certain person slipped and broke a leg in the middle of a dry season.
Thus Bayesian networks are particularly useful in studying higher cognitive functions, where the problem of organizing and supervising large assemblies of specialized neural networks becomes important.
Castillo, E., J. M. Gutierrez, and A. S. Hadi. (1997). Expert Systems and Probabilistic Network Models. New York: Springer.
Cooper, G. F., and E. Herskovits. (1990). A Bayesian method for constructing Bayesian belief networks from databases. Proceedings of the Conference on Uncertainty in AI, pp. 86-94.
Goldszmidt, M., and J. Pearl. (1996). Qualitative probabilities for default reasoning, belief revision, and causal modeling. Artificial Intelligence 84(1-2): 57 - 112.
Heckerman, D., A. Mamdani, and M. P. Wellman, Guest Eds., (1995). Real-world applications of Bayesian networks. Communications of the ACM 38(3):24-68.
Jensen, F. V. (1996). An Introduction to Bayesian Networks. New York: Springer.
Kim, J. H., and J. Pearl. (1983). A computational model for combined causal and diagnostic reasoning in inference systems. Proceedings of IJCAI-83, pp. 190-193. Karlsruhe, Germany.
Lauritzen, S. L., and D. J. Spiegelhalter. (1988). Local computations with probabilities on graphical structures and their application to expert systems. Journal of the Royal Statistical Society Series B 50(2):157-224.
Pearl, J. (1982). Reverend Bayes on inference engines: A distributed hierarchical approach. Proceedings of the AAAI National Conference on AI, pp. 133-136. Pittsburgh.
Pearl, J. (1987). Evidential reasoning using stochastic simulation of causal models. Artificial Intelligence 32(2):245-258.
Pearl, J. (1988). Probabilistic Reasoning in Intelligent Systems. San Mateo, CA: Morgan Kaufmann.
Pearl, J. (1996). Causation, action, and counterfactuals. In Y. Shoham, Ed., Theoretical Aspects of Rationality and Knowledge: Proceedings of the Sixth Conference. San Francisco: Morgan Kaufmann, pp. 51-73.
Pearl, J., and T. Verma. (1991). A theory of inferred causation. In J. A. Allen, R. Fikes, and E. Sandewall, Eds., Principles of Knowledge Representation and Reasoning: Proceedings of the Second International Conference. San Mateo, CA: Morgan Kaufmann, pp. 441-452.
Shafer, G., and J. Pearl, Eds. (1990). Readings in Uncertain Reasoning. San Mateo, CA: Morgan Kaufmann.
Spirtes, P., C. Glymour, and R. Schienes. (1993). Causation, Prediction, and Search. New York: Springer.
Spiegelhalter, D. J., and S. L. Lauritzen. (1990). Sequential updating of conditional probabilities on directed graphical structures. Networks: An International Journal 20(5):579-605 .