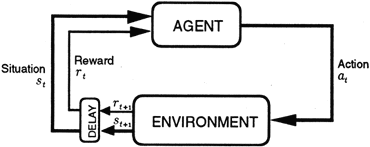
Figure 1 The Reinforcement learning framework.
Reinforcement learning is an approach to artificial intelligence that emphasizes learning by the individual from its interaction with its environment. This contrasts with classical approaches to artificial intelligence and MACHINE LEARNING, which have downplayed learning from interaction, focusing instead on learning from a knowledgeable teacher, or on reasoning from a complete model of the environment. Modern reinforcement learning research is highly interdisciplinary; it includes researchers specializing in operations research, genetic algorithms, NEURAL NETWORKS, psychology, and control engineering.
Reinforcement learning is learning what to do -- how to map situations to actions -- so as to maximize a scalar reward signal. The learner is not told which action to take, as in most forms of machine learning, but instead must discover which actions yield the most reward by trying them. In the most interesting and challenging cases, actions may affect not only the immediate reward but also the next situation, and through that all subsequent rewards. These two characteristics -- trial-and-error search and delayed reward -- are the two most important distinguishing features of reinforcement learning.
One of the challenges that arises in reinforcement learning and not in other kinds of learning is the trade-off between exploration and exploitation. To obtain a lot of reward, a reinforcement learning agent must prefer actions that it has tried in the past and found to be effective in producing reward. But to discover which actions these are it has to select actions that it has not tried before. The agent has to exploit what it already knows in order to obtain reward, but it also has to explore in order to make better action selections in the future. The dilemma is that neither exploitation nor exploration can be pursued exclusively without failing at the task.

Figure 1 The Reinforcement learning framework.
Modern reinforcement learning research uses the formal framework of Markov decision processes (MDPs). In this framework, the agent and environment interact in a sequence of discrete time steps, t = 0, 1, 2, 3, . . . On each step, the agent perceives the environment to be in a state, st, and selects an action, at. In response, the environment makes a stochastic transition to a new state, st+1, and stochastically emits a numerical reward, rt+1 ∈ ℜ (see figure 1). The agent seeks to maximize the reward it receives in the long run. For example, the most common objective is to choose each action at, so as to maximize the expected discounted return:
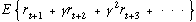
where γ is a discount-rate parameter, 0 ≤ γ ≤ 1, akin to an interest rate in economics. This framework is intended to capture in a simple way essential features of the problem of learning from interaction and thus of the overall problem of artificial intelligence. It includes sensation and action, cause and effect, and an explicit goal involving affecting the environment. There is uncertainty both in the environment (because it is stochastic) and about the environment (because the environment's transition probabilities may not be fully known). Simple extensions of this problem include incomplete perception of the state of the environment and computational limitations. Most theoretical results about reinforcement learning apply to the special case in which the state and action spaces are finite, in which case the process is called a finite MDP.
Reinforcement learning methods attempt to improve the agent's decision-making policy over time. Formally, a policy is a mapping from states to actions, or to probability distributions over actions. The policy is stored in a relatively explicit fashion so that appropriate responses can be generated quickly in response to unexpected states. The policy is thus what is sometimes called a "universal plan" in artificial intelligence, a "control law" in CONTROL THEORY, or a set of "stimulus-response associations" in psychology. We can define the value of being in a state s under policy π as the expected discounted return starting in that state and following policy π. The function mapping all states to their values is called the state-value function for the policy:
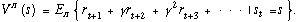
The values of states define a natural ordering on policies. Policy π is said to be better than or equal to policy π' iff Vπ(s) ≥ Vπ'(s) for all states s. For finite MDPs there are always one or more policies that are better than or equal to all others. These are the optimal policies, all of which share the same value function.
The simplest reinforcement learning algorithms apply directly to the agent's experience interacting with the environment, changing the policy in real time. For example, tabular one-step Q-learning, one of the simplest reinforcement learning algorithms, uses the experience of each state transition to update one element of a table. This table, denoted Q, has an entry, Q(s,a), for each pair of state, s, and action, a. Upon the transition st → st+ 1, having taken action and received reward rt+1, this algorithm performs the update
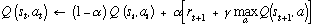
where α is a positive step-size parameter. Under appropriate conditions (ensuring sufficient exploration and reduction of α over time), this process converges such that the greedy policy with respect to Q is optimal. The greedy policy is to select in each state, s, the action, a, for which Q(s,a) is largest. Thus, this algorithm provides a way of finding an optimal policy purely from experience, with no model of the environment's dynamics.
The algorithm described above is only the simplest of reinforcement learning methods. More sophisticated methods implement Q not as a table, but as a trainable parameterized function such as an artificial neural network. This enables generalization between states, which can greatly reduce learning time and memory requirements. Another common extension, eligibility traces, allows credit for a good state transition to spread more quickly to the states that preceded it, again resulting in faster learning. Continuous-time reinforcement learning problems require eligibility traces just as continuous-state or continuous-action problems require parameterized function approximators.
Reinforcement learning is also a promising approach to PLANNING and PROBLEM SOLVING. In this case, a model of the environment is used to simulate extensive interaction between it and the agent. This simulated experience is then processed by reinforcement learning methods just as if it had actually occurred. The result is a sort of "anytime planning," in which the agent's policy gradually improves over time and computational effort. Reinforcement learning methods appear most suited to planning problems that are too large or stochastic to be solved by conventional methods such as HEURISTIC SEARCH or DYNAMIC PROGRAMMING. This approach has already proved very effective in applications, having produced the best of all known methods for playing backgammon, dispatching elevators, assigning cellular radio channels, and scheduling space shuttle payload processing.
Bertsekas, D. P., and J. N. Tsitsiklis. (1996). Neuro-Dynamic Programming. Belmont, MA: Athena Scientific.
Kaelbling, L. P., Ed. (1996). Special issue on reinforcement learning. Machine Learning 22(1-3).
Kaelbling, L. P., M. L. Littman, and A. W. Moore. (1996). Reinforcement learning: A survey. Journal of Artificial Intelligence Research 4:237-285.
Sutton, R. S., Ed. (1992). Special issue on reinforcement learning. Machine Learning 8.
Sutton, R. S., and A. G. Barto. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press.
Watkins, C. J. C. H., and P. Dayan. (1992). Q-learning. Machine Learning 8:279-292.