
The term lightness refers to the perceived whiteness or blackness of an opaque surface. The physical counterpart of lightness is reflectance, or the percentage of light a surface reflects. A good white surface reflects about ninety percent of the light that illuminates it, absorbing the rest; black reflects only about three percent. The eye, having no reflectance detectors, must compute lightness based only on the light reflected from the scene. But the intensity of light reflected from any given surface, called luminance, is a product of both its reflectance and the level of illumination. And although luminance thus varies with every change of illumination, lightness remains remarkably stable, an achievement referred to as lightness constancy.
There is a perceptual quality that corresponds to luminance called brightness. Brightness is to lightness as perception of visual angle is to perception of object size (see SPATIAL PERCEPTION). While brightness might be said to refer to our sensation of light intensity, lightness refers to a perceived property of the object itself and is essential to object recognition (see SURFACE PERCEPTION).
Despite the remarkable correlation between lightness and physical reflectance, neither the stimulus variable on which it is based nor the computation that finally produces lightness has been agreed upon. HELMHOLTZ (1866), recognizing that lightness cannot be based simply on luminance, argued that the level of illumination is unconsciously taken into account, but this approach has remained vague and unconvincing. Wallach (1948) avoided the whole issue of computing the illumination with the dramatically simple proposal that lightness depends on the ratio between the luminance of a surface and the luminance of its background. He demonstrated that such a local edge ratio predicts perceived lightness in very simple displays such as a disk surrounded by an annulus. And he observed that, even for complex images, luminance ratios, unlike absolute luminance values, tend to remain invariant when the illumination changes. Others (Hurvich and Jameson 1966; Cornsweet 1970), lured by the prospect of a physiological account of lightness, have sought to reduce Wallach's ratio findings to the neural mechanism of lateral inhibition.
Subsequent research has suggested that what gets encoded are luminance ratios at edges, not the absolute luminances of points, and that lateral inhibition plays a key role in the neural encoding of these ratios. But both Wallach's ratio principle and its physiological reduction are now viewed as much too simplistic an account of lightness. Recent work has dealt with three important limitations: (1) the computation is too local; (2) it produces large errors when applied to illuminance edges; and (3) only relative lightness values can be determined, unless an anchoring rule is also given.
1. The first of these can be illustrated in simultaneous lightness contrast, the familiar textbook illusion, shown in figure 1. On its face this contrast illusion appears to provide further evidence of the relational determination of lightness. But if lightness depended simply on local luminance ratios, the two targets should look as different as black and white. So, in fact, the very weakness of the illusion shows that lightness is not tied to background luminance as strongly as Wallach's ratio rule implies. Quantitative work (Gilchrist 1988) has shown that lightness is just as independent of background luminance as it is of illumination level and this appears to require the ability to compute luminance ratios between remote regions of the image. In the early 1970s several writers (Land and McCann 1971; Arend, Buehler, and Lockhead 1971; Whittle and Challands 1969) proposed a process of edge integration by which all edge ratios along a path between two remote regions are mathematically combined.

Figure 1. Simultaneous lightness contrast. Although this illusion shows an influence of the target/background luminance ratio, the weakness of the illusion shows that lightness is no simple product of that ratio.
2. Gilchrist (1979), noting that many edges in the retinal image represent changes in the illumination (such as shadow boundaries), not changes in reflectance, argued that edge integration cannot work without some prior process of edge classification (see figure 2). Recent computational models (Bergström 1977; Adelson 1993; Gilchrist 1979) have relied on concepts like edge integration and edge classification to decompose the retinal image into component images -- called intrinsic images -- that represent the physical values of surface reflectance and illumination. This approach has the advantage of providing an account of our perception of the illumination, not just of surface lightness.
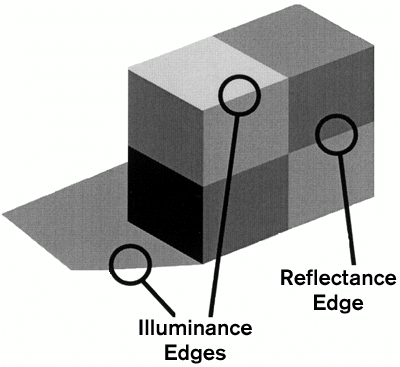
Figure 2. Lightness could not be based on local edge ratios unless the edges were first classified. (After Adelson 1993.)
3. Computing absolute or specific shades of gray requires an anchoring rule, a rule that ties some locus on the scale of perceived grays to some feature of the retinal image. One candidate rule, endorsed by Wallach (1948) and by Land and McCann (1971), says that the highest luminance is white, with lower luminances scaled relative to this standard. An alternative rule, implicit in concepts like the gray world assumption and Helson's adaptation-level theory (1964), says that the average luminance is middle gray, with higher and lower values scaled relative to the average. When these rules are tested by presenting a display consisting of a very restricted range of grays, it is found that the highest luminance appears white, but the average does not appear middle gray (Cataliotti and Gilchrist 1995; Li and Gilchrist in press). But relative area also plays an important role. An increase in the area of the darker regions at the expense of the lighter causes the darker regions to lighten in gray value and the lightest region to appear self-luminous.
These rules of anchoring by highest luminance and relative area apply to both simple visual displays and to frameworks or groups embedded within complex images. In complex images, however, perceived lightness can be predicted by a compromise between lightness values computed within these relatively local frameworks and lightness values computed across the entire visual field. The weighting in this compromise increasingly shifts to the local framework as that becomes larger and more highly articulated. If the study of anchoring has undermined the portrait of a highly ratiomorphic lightness computation recovering veridical values of reflectance and illumination, it has nevertheless provided a remarkable account of perceptual errors. Emerging anchoring models portray a more rough-and-ready system (see MID-LEVEL VISION) that, while subject to apparently unnecessary errors, is nevertheless quite robust in the face of a wide variety of challenges to perceptual veridicality.
Adelson, E. (1993). Perceptual organization and the judgment of brightness. Science 262:2042-2044.
Arend, L. E., J. N. Buehler, and G. R. Lockhead. (1971). Difference information in brightness perception. Perception and Psychophysics 9:367-370.
Bergström, S. S. (1977). Common and relative components of reflected light as information about the illumination, colour, and three-dimensional form of objects. Scandinavian Journal of Psychology 18:180-186.
Cataliotti, J., and A. L. Gilchrist. (1995). Local and global processes in lightness perception. Perception and Psychophysics 57(2):125-135.
Cornsweet, T. N. (1970). Visual Perception. New York: Academic Press.
Gilchrist, A. (1979). The perception of surface blacks and whites. Scientific American 240:112-123.
Gilchrist, A. (1988). Lightness contrast and failures of constancy: a common explanation. Perception and Psychophysics 43(5):415-424.
Helmholtz, H. von. (1866/1924). Helmholtz's Treatise on Physiological Optics. New York: Optical Society of America.
Helson, H. (1964). Adaptation-Level Theory. New York: Harper and Row.
Hurvich, L., and D. Jameson. (1966). The Perception of Brightness and Darkness. Boston: Allyn and Bacon.
Land, E. H., and J. J. McCann. (1971). Lightness and retinex theory. Journal of the Optical Society of America 61:1-11.
Li, X., and A. Gilchrist. (Forthcoming). Relative area and relative luminance combine to anchor surface lightness values. Perception and Psychophysics.
Wallach, H. (1948). Brightness constancy and the nature of achromatic colors. Journal of Experimental Psychology 38:310-324.
Whittle, P., and P. D. C. Challands. (1969). The effect of background luminance on the brightness of flashes. Vision Research 9:1095-1110.
Gilchrist, A., Ed. (1994). Lightness, Brightness, and Transparency. Hillsdale, NJ: Erlbaum.
Gilchrist, A., C. Kossyfidis, F. Bonato, T. Agostini, J. Cataliotti, X. Li, B. Spehar, V. Annan, and E. Economou. (Forthcoming). An anchoring theory of lightness perception. Psychological Review.
Hurlbert, A. (1986). Formal connections between lightness algorithms. Journal of the Optical Society of America A. Optics and Image Science 3:1684-1693.
Koffka, K. (1935). Principles of Gestalt Psychology. New York: Harcourt, Brace, and World, pp. 240-264.
MacLeod, R. B. (1932). An experimental investigation of brightness constancy. Archives of Psychology 135:5-102.
Wallach, H. (1976). On Perception. New York: Quadrangle/The New York Times Book Co .