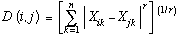
An ability to assess similarity lies close to the core of cognition. In the time-honored tradition of legitimizing fields of psychology by citing William JAMES, "This sense of Sameness is the very keel and backbone of our thinking" (James 1890/1950: 459). An understanding of PROBLEM SOLVING, categorization, memory retrieval, inductive reasoning, and other cognitive processes requires that we understand how humans assess similarity. Four major psychological models of similarity are geometric, featural, alignment-based, and transformational.
Geometric models have been among the most influential approaches to analyzing similarity (Torgerson 1965), and are exemplified by multidimensional scaling (MDS) models (Nosofsky 1992; Shepard 1962). The input to MDS routines may be similarity judgments, confusion matrices (a table of how often each entity is confused with every other entity), probabilities of entities being grouped together, or any other measure of subjective similarity between all pairs of entities in a set. The output of an MDS routine is a geometric model of the entities' similarity, with each entity of the set represented as a point in N-dimensional space. The similarity of two entities i and j is taken to be inversely related to their distance, D(i, j), which is computed by
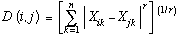
where n is the number of dimensions, Xik is the value of dimension k for entity i, and r is a parameter that allows different spatial metrics to be used. A Euclidean metric (r = 2) often provides good fits to human similarity judgments when the entities are holistically perceived or the underlying dimensions are psychologically fused, whereas a city-block metric (r = 1) often provides a better fit when entities are clearly divisible into separate dimensions (Garner 1974). Shepard (1987) has made a compelling case that cognitive assessments of similarity are related by an inverse exponential function to distance in MDS space.
Geometric models standardly assume minimality [D(A, B) ≥ D(A, A) = 0 ], symmetry [ D(A, B) = D(B, A) ], and the triangle inequality [ D(A, B) + D(B, C) ≥ D(A, C) ]. Amos TVERSKY (1977) criticized geometric models on the grounds that violations of all three assumptions are empirically observed. Minimality may be violated because not all identical objects seem equally similar; complex objects that are identical (e.g., twins) can be more similar to each other than simpler identical objects (e.g., two squares). Asymmetrical similarity occurs when an object with many features is judged as less similar to a sparser object than vice versa; for example, North Korea is judged to be more like China than China is to North Korea (Tversky 1977). The triangle inequality can be violated when A (e.g., "lamp") and B ("moon") share an identical feature (both provide light), and B ("moon") and C ("ball") share an identical feature, but A and C share no feature in common (Tversky and Gati 1982).
Although geometric models can be modified to correct these assumptions (Nosofsky 1991), Tversky suggested an alternative approach, the contrast model, wherein similarity is determined by matching features of compared entities, and integrating these features by the formula
S(A,B) = θ f(A ∩ B) - α f(A-B) - β f(B-A).
The similarity of A to B, S(A,B) is expressed as a linear combination of the measure of the common and distinctive features. The term (A ∩ B) represents the features that items A and B have in common. (A - B) represents the features that A has but B does not. (B - A) represents the features that B, but not A, possesses. The terms θ, α, and β reflect the weights given to the common and distinctive components, and the function f is often simply assumed to be additive. Other featural models calculate similarity by taking the ratio of common to distinctive features (Sjoberg 1972).
Neither geometric nor featural models of similarity are well suited for comparing things that are richly structured rather than just being a collection of coordinates or features. Often it is most efficient to represent things hierarchically (parts containing parts) and/or propositionally (relational predicates taking arguments). In such cases, comparing things involves not simply matching features, but determining which elements correspond to, or align with, one another. Matching features are aligned to the extent that they play similar roles within their entities. For example, a car with a green wheel and a truck with a green hood both share the feature green, but this matching feature may not increase their similarity much because the car's wheel does not correspond to the truck's hood. Drawing inspiration from work on analogical reasoning (Gentner 1983; Holyoak and Thagard 1989; see ANALOGY), in alignment-based models, matching features influence similarity more if they belong to parts that are placed in correspondence, and parts tend to be placed in correspondence if they have many features in common and if they are consistent with other emerging correspondences (Goldstone 1994; Markman and Gentner 1993).
A fourth approach to modeling similarity is based on transformational distance. The similarity of two entities is assumed to be inversely proportional to the number of operations required to transform one entity so as to be identical to the other (Hahn and Chater 1997; Imai 1977). For example, XXXXO requires only one transformation to become XXXOO (change an O to an X), but requires two transformations to become OOXXX (change an O to an X, and reverse string), and consequently is more similar to XXXOO.
Although testing between these four approaches to similarity is an ongoing topic of research, another major issue concerns the role of similarity in other cognitive processes. For example, although several models of categorization are completely similarity-based (see CONCEPTS and CATEGORIZATION), other researchers have argued that people's categorizations cannot be exhaustively explained by similarity but also depend on abstract, theoretical knowledge (Rips and Collins 1993; Murphy and Medin 1985). Likewise, Goodman (1972) raised philosophical objections to the explanatory role of similarity, arguing that "X is similar to Y . . ." is totally unconstrained until it is completed by "with respect to property Z," and that it is this latter clause that performs all of the explanatory work. However, other researchers have argued that even without the additional clause, similarity is constrained by perceptual processes, by the manner in which multiple properties are integrated together (Goldstone 1994), by the compared items themselves (Medin, Goldstone, and Gentner 1993), by default properties that are applied irrespective of context (Barsalou 1982), and by a natural tendency to perceive overall similarity across many properties rather than similarity with respect to a single property (Smith 1989).
Another caveat to the explanatory role of similarity is that similarity may not be a unitary phenomenon. Similarity assessments are influenced by context, perspective, choice alternatives, and expertise (Medin, Goldstone, and Gentner 1993; Tversky 1977). Different processes for assessing similarity are probably used for different tasks, domains, and stimuli. The choice of features, transformations, and structural descriptions used to describe entities will govern the predictions made by similarity models as much as do the model's mechanisms for comparing and integrating these representations. History has not supported a literal interpretation of Fred Attneave's (1950: 516) claim, "The question 'What makes things seem alike or seem different?' is one so fundamental to psychology that very few psychologists have been naive enough to ask it" in that the topic has inspired considerable research, but this research has vindicated Attneave at a deeper level by testifying to the importance and complexity of similarity.
Barsalou, L. W. (1982). Context-dependent and context-independent information in concepts. Memory and Cognition 10:82-93.
Attneave, F. (1950). Dimensions of similarity. American Journal of Psychology 63:516-556.
Garner, W. R. (1974). The Processing of Information and Structure. New York: Wiley.
Gentner, D. (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science 7:155-170.
Goldstone, R. L. (1994). Similarity, interactive activation, and mapping. Journal of Experimental Psychology: Learning, Memory, and Cognition 20:3-28.
Goldstone, R. L. (1994). The role of similarity in categorization: Providing a groundwork. Cognition 52:125-157.
Goodman, N. (1972). Seven strictures on similarity. In N. Goodman, Ed., Problems and Projects. New York: Bobbs-Merrill, pp. 23-32.
Hahn, U., and N. Chater. (1997). Concepts and similarity. In L. Lamberts and D. Shanks, Eds., Knowledge, Concepts, and Categories. Hove, UK: Psychology Press/MIT Press.
Holyoak, K. J., and P. Thagard. (1989). Analogical mapping by constraint satisfaction. Cognitive Science 13:295-355.
Imai, S. (1977). Pattern similarity and cognitive transformations. Acta Psychologica 41:433-447.
James, W. (1890/1950). The Principles of Psychology. Dover: New York. (Original work published 1890.)
Markman, A. B., and D. Gentner. (1993). Structural alignment during similarity comparisons. Cognitive Psychology 25:431-467.
Medin, D. L., R. L. Goldstone, and D. Gentner. (1993). Respects for similarity. Psychological Review 100:254-278.
Murphy, G. L., and D. L. Medin. (1985). The role of theories in conceptual coherence. Psychological Review 92:289-316.
Nosofsky, R. M. (1991). Stimulus bias, asymmetric similarity, and classification. Cognitive Psychology 23:94-140.
Nosofsky, R. M. (1992). Similarity scaling and cognitive process models. Annual Review of Psychology 43:25-53.
Rips, L. J., and A. Collins. (1993). Categories and resemblance. Journal of Experimental Psychology: General 122:468-486.
Shepard, R. N. (1962). The analysis of proximities: Multidimensional scaling with an unknown distance function. Part 1. Psychometrika 27:125-140.
Shepard, R. N. (1987). Toward a universal law of generalization for psychological science. Science 237:1317-1323.
Sjoberg, L. (1972). A cognitive theory of similarity. Goteborg Psychological Reports 2(10).
Smith, L. B. (1989). From global similarity to kinds of similarity: The construction of dimensions in development. In S. Vosniadu and A. Ortony, Eds., Similarity and Analogical Reasoning. Cambridge: Cambridge University Press, pp. 146-178.
Torgerson, W. S. (1965). Multidimensional scaling of similarity. Psychometrika 30:379-393.
Tversky, A. (1977). Features of similarity. Psychological Review 84:327-352.
Tversky, A., and I. Gati. (1982). Similarity, separability, and the triangle inequality. Psychological Review 89:123-154.
Asbhy, F. G. (1992). Multidimensional Models of Perception and Cognition. Hillsdale, NJ: Erlbaum.
Ashby, F. G., and N. A. Perrin. (1988). Toward a unified theory of similarity and recognition. Psychological Review 95:124-150.
Edelman, S. (Forthcoming). Representation is representation of similarity. Behavioral and Brain Sciences to appear.
French, R. (1995). The Subtlety of Sameness. Cambridge, MA: MIT Press.
Goldstone, R. L., D. L. Medin, and J. Halberstadt. (1997). Similarity in Context. Memory and Cognition 25:237-255.
Hofstadter, D., and The Fluid Analogies Research Group. (1995). Fluid Concepts and Creative Analogies. New York: Basic Books.
Indurkhya, B. (1992). Metaphor and Cognition. Dordrecht: Kluwer.
Keil, F. C. (1989). Concepts, Kinds and Development. Cambridge, MA: MIT Press.
Krumhansl, C. L. (1978). Concerning the applicability of geometric models to simiarity data: The interrelationship between similarity and spatial density. Psychological Review 85:450-463.
Lantermann, E. D., Ed. (1980). Similarity and Choice. New York: Burgess.
Link, S. W. (1992). The Wave Theory of Difference and Similarity. Newark, NJ: Erlbaum.
Melara, R. D. (1992). The concept of perceptual similarity: From psychophysics to cognitive psychology. In D. Algom, Ed., Psychophysical Approaches to Cognition. Amsterdam: North- Holland, pp. 303-388.
Ramscar, M., U. Hahn, E. Cambouropulos, and H. Pain, Eds. (1997). Proceedings of the Interdisciplinary Workshop on Similarity and Categorization. Edinburgh: Department of Artificial Intelligence, University of Edinburgh.
Sloman, S. A. (1996). The empirical case for two systems of reasoning. Psychological Bulletin 119:3-22.
Vosniadu, S., and A. Ortony. (1989). Similarity and Analogical Reasoning. Cambridge: Cambridge University Press.