Heuristic Search
Heuristic
search is the study of computer algorithms designed for PROBLEM SOLVING, based on trial-and-error exploration of possible
solutions. Problem solving tasks include "pathfinding problems," game
playing, and CONSTRAINT SATISFACTION.
The task of navigating in a network
of roads from an initial location to a desired goal location, with
the aid of a roadmap, is an example of a pathfinding problem. The "states" of
the problem are decision points, or intersections of two or more
roads. The "operators" are segments of road between
two adjacent intersections. The navigation problem can be viewed
as finding a sequence of operators (road segments) that go from
the initial state (location) to the goal state (location). In a
game such as CHESS, the states are the legal
board configurations, and the operators are the legal moves.
A search algorithm may be systematic
or nonsystematic. A systematic algorithm is guaranteed to find a
solution if one exists, and may in fact guarantee a lowest-cost
solution. Nonsystematic algorithms, such as GREEDY LOCAL SEARCH, EVOLUTIONARY COMPUTATION, and other stochastic
approaches, are not guaranteed to find a solution. We focus on systematic
algorithms here.
The simplest systematic algorithms,
called "brute-force search" algorithms, do not
use any knowledge about the problem other than the states, operators,
and initial and goal states. For example, "breadth-first
search" starts with the initial state, then considers all
states one operator away from the initial state, then all states
two operators away, and so on until the goal is reached. Uniform-cost
search, or Dijkstra's algorithm (Dijkstra 1959), considers
the different costs of operators, or lengths of road segments in
our example, and visits the states in increasing order of their
distance from the start. A drawback of both these algorithms is
that they require enough memory to hold all the states considered
so far, which is prohibitive in very large problems (see the following).
"Depth-first search" more
closely approximates how one would search if actually driving in
the road network, rather than planning with a map. From the current
location, depth-first search extends the current path by following
one of the roads until a dead end is reached. It then backtracks
to the last decision point that has not been completely explored,
and chooses a new path from there. The advantage of depth-first
search is that it only requires enough memory to hold the current
path from the initial state.
"Bi-directional search" (Pohl
1971) searches forward from the initial state and backward from
the goal state simultaneously, until the two searches meet. At that
point, a complete path from the initial state to the goal state
has been found.
A drawback of all brute-force searches
is the amount of time they take to execute. For example, a breadth-first
search of a road network will explore a roughly circular region
whose center is the initial location, and whose radius is the distance
to the goal. It has no sense of where the goal is until it stumbles upon
it.
Heuristic search, however, is directed
toward the goal. A heuristic search, such as the "A* algorithm" (Hart,
Nilsson, and Raphael 1968), makes use of a "heuristic evaluation
function," which estimates the distance from any location
to the goal. For example, the straight-line distance from a given location
to the goal is often a good estimate of the actual road distance.
For every location visited by A*, it estimates
the total distance of a path to the goal that passes through that
location. This is the sum of the distance from the start to the
location, plus the straight-line distance from the location to the
goal. A* starts with the initial location, and
generates all the locations immediately adjacent to it. It then
evaluates these locations in the above way. At each step, it generates
and evaluates the neighbors of the unexplored location with the
lowest total estimate. It stops when it chooses a goal location.
A* is guaranteed
to find a solution if one exists. Furthermore, if the heuristic
function never overestimates actual cost, A* is
guaranteed to find a shortest solution. For example, because the
shortest path between two points is a straight line, A* using
the straight-line distance heuristic function is guaranteed to find a
shortest solution to the road navigation problem.
The bane of all search algorithms
is called "combinatorial explosion." In road navigation,
the total number of intersections is quite manageable for a computer.
Consider, however, the traveling salesman problem (TSP). Given a
set of N cities, the TSP is to find a shortest tour that
visits all the cities and returns to the starting city. Given N cities,
there are (N - 1)! different orders in which the
cities could be visited. Clever algorithms can reduce the number
of possibilities to 2N,
but even if N is as small as 50, 2N is
approximately 1015. Even
if a computer could examine a million possibilities per second,
examining 1015 possibilities
would take 31.7 years.
An algorithm that is well suited
to problems such as the TSP is called depth-first branch-and-bound.
A TSP solution is a sequence of cities. Depth-first branch-and-bound
systematically searches the possible tours depth-first, adding one city
at a time to a partial tour, and backtracks when a tour is completed.
In addition, it keeps track of the length of the shortest complete
tour found so far, in a variable 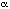 .
Whenever a partial tour is found in which the sum of the trip segments already
included exceeds
.
Whenever a partial tour is found in which the sum of the trip segments already
included exceeds 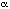 , we need not consider
any extensions of that partial tour, inasmuch as the total cost
can only be greater. In addition, a heuristic evaluation function
can be used to estimate the cost of completing a partial tour. If
the heuristic function never overestimates the lowest completion
cost, whenever the cost of the segments so far, plus the heuristic
estimate of the completion cost, exceeds
, we need not consider
any extensions of that partial tour, inasmuch as the total cost
can only be greater. In addition, a heuristic evaluation function
can be used to estimate the cost of completing a partial tour. If
the heuristic function never overestimates the lowest completion
cost, whenever the cost of the segments so far, plus the heuristic
estimate of the completion cost, exceeds 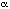 ,
we can backtrack. All known algorithms that are guaranteed to find
an optimal solution to such "combinatorial problems" are variants
of branch-and-bound.
,
we can backtrack. All known algorithms that are guaranteed to find
an optimal solution to such "combinatorial problems" are variants
of branch-and-bound.
See also
Additional links
-- Richard Korf
References
Dijkstra, E. W. (1959). A note on two problems
in connexion with graphs. Numerische Mathematik 1:269-271.
Hart, P. E., N. J. Nilsson, and B. Raphael.
(1968). A formal basis for the heuristic determination of minimum
cost paths. IEEE Transactions on Systems Science and Cybernetics 4(2):100-107.
Pohl, I. (1971). Bi-directional search. In B.
Meltzer and D. Michie, Eds., Machine Intelligence 6. New
York: American Elsevier, pp. 127-140.
Further Readings
Bolc, L., and J. Cytowski. (1992). Search
Methods for Artificial Intelligence. London: Academic Press.
Kanal, L., and V. Kumar, Eds. (1988). Search
in Artificial Intelligence. New York: Springer.
Korf, R. E. (1985). Depth-first iterative-deepening:
an optimal admissible tree search. Artificial Intelligence 27(1):97-109.
Korf, R. E. (1998). Artificial intelligence
search algorithms. To appear in M. J. Atallah, Ed., CRC Handbook
of Algorithms and Theory of Computation. Boca Raton, FL:
CRC Press.
Newell, A., and H. A. Simon. (1972). Human
Problem Solving. Englewood Cliffs, NJ: Prentice-Hall.
Pearl, J. (1984). Heuristics. Reading,
MA: Addison-Wesley.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
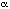 .
Whenever a partial tour is found in which the sum of the trip segments already
included exceeds
.
Whenever a partial tour is found in which the sum of the trip segments already
included exceeds 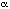 , we need not consider
any extensions of that partial tour, inasmuch as the total cost
can only be greater. In addition, a heuristic evaluation function
can be used to estimate the cost of completing a partial tour. If
the heuristic function never overestimates the lowest completion
cost, whenever the cost of the segments so far, plus the heuristic
estimate of the completion cost, exceeds
, we need not consider
any extensions of that partial tour, inasmuch as the total cost
can only be greater. In addition, a heuristic evaluation function
can be used to estimate the cost of completing a partial tour. If
the heuristic function never overestimates the lowest completion
cost, whenever the cost of the segments so far, plus the heuristic
estimate of the completion cost, exceeds 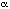 ,
we can backtrack. All known algorithms that are guaranteed to find
an optimal solution to such "combinatorial problems" are variants
of branch-and-bound.
,
we can backtrack. All known algorithms that are guaranteed to find
an optimal solution to such "combinatorial problems" are variants
of branch-and-bound.