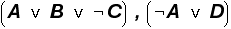Constraint Satisfaction

A constraint satisfaction problem (CSP) is defined over a constraint network, which consists of a finite set of variables, each associated with a domain of values, and a set of constraints. A solution is an assignment of a value to each variable from its domain such that all the constraints are satisfied. Typical constraint satisfaction problems are to determine whether a solution exists, to find one or all solutions, and to find an optimal solution relative to a given cost function. A well-known example of a constraint satisfaction problem is k-colorability, where the task is to color, if possible, a given graph with k colors only, such that any two adjacent nodes have different colors. A constraint satisfaction formulation of this problem associates the nodes of the graph with variables, the possible colors are their domains, and the inequality constraints between adjacent nodes are the constraints of the problem. Each constraint of a CSP may be expressed as a relation, defined on some subset of variables, denoting legal combinations of their values. Constraints can also be described by mathematical expressions or by computable procedures. Another typical constraint satisfaction problem is SATisfiability, the task of finding the truth assignment to propositional variables such that a given set of clauses is satisfied. For example, given the two clauses 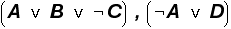, the assignment of falseto A,trueto B,falseto C, and falseto D, is a satisfying truth value assignment.

The structure of a constraint network is depicted by a constraint graph whose nodes represent the variables and in which any two nodes are connected if the corresponding variables participate in the same constraint. In the k-colorability formulation, the graph to be colored is the constraint graph. In our SAT example the constraint graph has A connected to D, and A, B, and C are connected to each other.

Constraint networks have proven successful in modeling mundane cognitive tasks such as vision, language comprehension, default reasoning, and abduction, as well as in applications such as scheduling, design, diagnosis, and temporal and spatial reasoning. In general, constraint satisfaction tasks are computationally intractable ("NP-hard"; see COMPUTATIONAL COMPLEXITY).

ALGORITHMS for processing constraints can be classified into two interacting categories: (1) search and (2) consistency inference. Search algorithms traverse the space of partial instantiations, while consistency inference algorithms reason through equivalent problems. Search algorithms are either systematic and complete or stochastic and incomplete. Likewise, consistency inference algorithms have either complete solutions (e.g., variable-elimination algorithms) or incomplete solutions (i.e., local consistency algorithms).

Local consistency algorithms, also called "consistency-enforcing" or "constraint propagation" algorithms (Montanari 1974; Mackworth 1977; Freuder 1982), are polynomial algorithms that transform a given constraint network into an equivalent, yet more explicit network by deducing new constraints to be added onto the network. Intuitively, a consistency-enforcing algorithm will make any partial solution of a small subnetwork extensible to some surrounding network. For example, the most basic consistency algorithm, called an "arc consistency" algorithm, ensures that any legal value in the domain of a single variable has a legal match in the domain of any other selected variable. A "path consistency" algorithm ensures that any consistent solution to a two-variable subnetwork is extensible to any third variable, and, in general, i-consistency algorithms guarantee that any locally consistent instantiation of i - 1 variables is extensible to any ith variable. Enforcing i-consistency is time and space exponential in i. Algorithms for i-consistency frequently decide inconsistency.

A network is globally consistent if it is i-consistent for every i, which means a solution can be assembled by assigning values using any variable ordering without encountering any dead end, namely, in a "backtrack-free" manner. However, it is enough to possess directional global consistency relative to a given ordering only. Indeed, an adaptive consistency (variable elimination) algorithm enforces global consistency in a given order only, such that every solution can be extracted, with no dead ends along this ordering. Another related algorithm, called a "tree-clustering" algorithm, compiles the given constraint problem into an equivalent tree of subproblems (Dechter and Pearl 1989) whose respective solutions can be efficiently combined into a complete solution. Adaptive consistency and tree-clustering algorithms are time and space exponential in a parameter of the constraint graph called an "induced-width" or "tree-width" (Arnborg and Proskourowski 1989; Dechter and Pearl 1987).

When a problem is computationally hard for the adaptive consistency algorithm, it can be solved by bounding the amount of consistency enforcing (e.g., arc or path consistency), and by augmenting the algorithm with a search component. Generally speaking, search will benefit from network representations that have a high level of consistency. However, because the complexity of enforcing i-consistency is exponential in i, there is a trade-off between the effort spent on consistency inference and that spent on search. Theoretical and empirical studies of this trade-off, prior to or during search, aim at identifying a problem-dependent cost-effective balance (Haralick and Elliot 1980; Prosser 1993; Sabin and Freuder 1994; Dechter and Rish 1994).

The most common algorithm for performing systematic search is the backtracking algorithm, which traverses the space of partial solutions in a depth-first manner. At each step, the algorithm extends a partial solution by assigning a value to one more variable. When a variable is encountered such that none of its values are consistent with the partial solution (a situation referred to as a "dead end"), backtracking takes place. The algorithm is time exponential, but requires only linear space.

Improvements of the backtracking algorithm have focused on the two phases of the algorithm: moving forward (look-ahead schemes) and backtracking (look-back schemes; Dechter 1990). When moving forward, to extend a partial solution, some computation (e.g., arc consistency) is carried out to decide which variable and value to choose next. For variable orderings, variables that maximally constrain the rest of the search space are preferred. For value selection, however, the least constraining value is preferred, in order to maximize future options for instantiations (Haralick and Elliot 1980; Dechter and Pearl 1987; Purdom 1983; Sabin and Freuder 1994).

Look-back schemes are invoked when the algorithm encounters a dead end. These schemes perform two functions: (1) they decide how far to backtrack, by analyzing the reasons for the dead end, a process often referred to as "backjumping" (Gaschnig 1979); (2) they record the reasons for the dead end in the form of new constraints so that the same conflicts will not arise again, a process known as "constraint learning" and "no-good recording" (Stallman and Sussman 1977; Dechter 1990).

Stochastic local search strategies have been recently reintroduced into the satisfiability and constraint satisfaction literature under the umbrella name (GSAT "greedy SATisfiability"; see GREEDY LOCAL SEARCH). These methods move in hill-climbing manner in the space of complete instantiations to all the variables (Minton et al. 1990). The algorithm improves its current instantiation by "flipping" a value of a variable that maximizes the number of constraints satisfied. Such search algorithms are incomplete, may get stuck in a local maxima, and cannot prove inconsistency. Nevertheless, when equipped with some heuristics for randomizing the search walksat or for revising the guiding criterion function (constraint reweighting), they prove successful in solving large and hard problems that are frequently hard for backtracking search algorithms (Selman, Levesque, and Mitchell 1992).

Structure-driven algorithms cut across both search and consistency inference algorithms. These techniques emer-ged from an attempt to topologically characterize constraint problems that are tractable. Tractable classes were generally recognized by realizing that enforcing low-level consistency (in polynomial time) guarantees global consistency for some problems. The basic network structure that supports tractability is a tree (Mackworth and Freuder 1985). In particular, enforcing arc consistency on a tree-structured network ensures global consistency along some ordering. Most other graph-based techniques can be viewed as transforming a given network into a metatree. Adaptive consistency, tree clustering, and constraint learning, are all time and space exponentially bounded by the tree width of the constraint graph; the cycle cutset scheme combines search and inference and is exponentially bounded by the constraint graph's cycle-cutset; the biconnected component method is bounded by the size of the constraint graph's largest biconnected component (Freuder 1982); and backjumping is exponentially bounded by the depth of the graph's depth-first search tree. The last three methods require only polynomial space.

Tractable classes were also identified by the properties of the constraints themselves. Such tractable classes exploit notions such as tight domains and tight constraints (van Beek and Dechter 1997), row-convex constraints (van Beek and Dechter 1995), implicational and max-ordered constraints (Kirousis 1993; Jeavons, Cohen, and Gyssens 1997), as well as causal networks. A connection between tractability and algebraic closure was recently discovered (Cohen, Jeavons, and Gyssens 1995) .

Finally, special classes of tractable constraints associated with TEMPORAL REASONING have received much attention in the last decade. These include subsets of qualitative interval algebra (Golumbic and Shamir 1993) expressing relationships such as "time interval A overlaps or precedes time interval B," as well as quantitative binary linear inequalities over the real numbers of the form X - Y 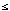a (Dechter, Meiri, and Pearl 1990).

Theoretical evaluation of constraint satisfaction algorithms is accomplished primarily by worst-case analysis (i.e., determining a function of the problem's size that sets the upper bound to the algorithm's performance over all problems of that size), or by dominance relationships (Kondrak and van Beek 1997). However, because worst-case analysis by its nature is too pessimistic and often does not reflect actual performance, empirical evaluation is necessary. Normally, a proposed algorithm is evaluated empirically on a set of randomly generated instances taken from the relatively "hard" "phase transition" region (Selman, Levesque, and Mitchell 1992). Other benchmarks based on real-life applications such as scheduling are also used. Currently, dynamic variable ordering and value selection heuristics that use various forms of constraint inference, backjumping, and constraint learning have been shown to be very effective for various problem classes (Prosser 1993; Frost and Dechter 1994; Sabin and Freuder 1994).

Additional links

-- Rina Dechter

References

Arnborg, S., and A. Proskourowski. (1989). Linear time algorithms for NP-hard problems restricted to partial k-trees. Discrete and Applied Mathematics 23:11-24.

Dechter, R. (1990). Enhancement schemes for constraint processing: Backjumping, learning, and cutset decomposition. Artificial Intelligence 41:273-312.

Dechter, R., and J. Pearl. (1987). Network-based heuristics for constraint satisfaction problems. Artificial Intelligence 34:1-38.

Dechter, R., and J. Pearl. (1989). Tree clustering for constraint networks. Artificial Intelligence 38(3):353-366.

Dechter, R., I. Meiri, and J. Pearl. (1990). Temporal constraint networks. Artificial Intelligence 49:61-95.

Dechter, R., and I. Rish. (1994). Directional resolution: The Davis-Putnam procedure, revisited. In Principles of Knowledge Representation and Reasoning, pp. 134-145.

Freuder, E. C. (1982). A sufficient condition for backtrack-free search. Journal of the ACM 29(1):24-32.

Frost, D., and R. Dechter. (1994). In search of best search: An empirical evaluation. In AAAI -94: Proceedings of the Twelfth National Conference on Artificial Intelligence. Seattle, WA, pp. 301-306.

Gaschnig, J. (1979). Performance Measurement and Analysis of Search Algorithms. Pittsburgh: Carnegie Mellon University.

Golumbic, M. C., and R. Shamir. (1993). Complexity and algorithms for reasoning about time: A graph-theoretic approach. Journal of the ACM 40:1108-1133.

Haralick, M., and G. L. Elliot. (1980). Increasing tree-search efficiency for constraint satisfaction problems. Artificial Intelligence 14:263-313.

Jeavons, P., D. Cohen, and M. Gyssens. (1997). Closure properties of constraints. Journal of ACM 44:527-548.

Kirousis, L. M. (1993). Fast parallel constraint satisfaction. Artificial Intelligence 64:147-160.

Kondrak, G., and P. van Beek. (1997). A theoretical valuation of selected algorithms. Artificial Intelligence 89:365-387.

Mackworth, A. K. (1977). Consistency in networks of relations. Artificial Intelligence 8(1):99-118.

Mackworth, A. K., and E. C. Freuder. (1985). The complexity of some polynomial network consistency algorithms for constraint satisfaction problems. Artificial Intelligence 25.

Minton, S., M. D. Johnson, A. B. Phillips, and P. Laird. (1990). Solving large-scale constraint satisfaction and scheduling problems using heuristic repair methods. In National Conference on Artificial Intelligence, Anaheim, CA, pp. 17-24.

Montanari, U. (1974). Networks of constraints: fundamental properties and applications to picture processing. Information Sciences 7(66):95-132.

Prosser, P. (1993). Hybrid algorithms for constraint satisfaction problems. Computational Intelligence 9(3):268-299.

Purdom, P. W. (1983). Search rearrangement backtracking and polynomial average time. Artificial Intelligence 21:117-133.

Sabin, D., and E. C. Freuder. (1994). Contradicting conventional wisdom in constraint satisfaction. In ECAI -94, Amsterdam, pp. 125-129.

Selman, B., H. Levesque, and D. Mitchell. (1992). A new method for solving hard satisfiability problems. In Proceedings of the Tenth National Conference on Artificial Intelligence, 339-347.

Stallman, M., and G. J. Sussman. (1977). Forward reasoning and dependency-directed backtracking in a system for computer-aided circuit analysis. Artificial Intelligence 2:135-196.

van Beek, P., and R. Dechter. (1995). On the minimality and decomposability of row-convex constraint networks. Journal of the ACM 42:543-561.

van Beek, P., and R. Dechter. (1997). Constraint tightness and looseness versus local and global consistency. Journal of the ACM 44(4):549-566.

Constraint Satisfaction

See also

Additional links

References

Further Readings