Signal Detection Theory

Signal detection theory (SDT) is a model of perceptual DECISION MAKING whose central tenet is that cognitive performance, limited by inherent variability, requires a decision process. Applying a statistical-decision approach developed in studying radar reception, W. P. Tanner and J. A. Swets proposed in 1954 a "decision-making theory of visual detection," showing how sensory and decision processes could be separated in the simplest perceptual task. Extensive early application to detection problems accounts for the name of the theory, but SDT is now used widely in cognitive science as a modeling tool and for analyzing discrimination and classification data (see PSYCHOPHYSICS).

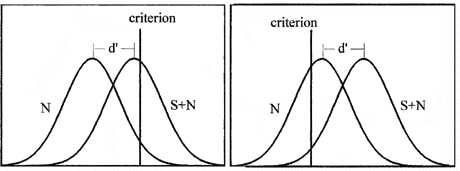
In detection, an observer attempts to distinguish two stimuli, noise (N) and signal plus noise (S + N). These stimuli evoke not single percepts, but trial-to-trial distributions of effects on some relevant decision axis, as in figure 1a. The observer's ability to tell the stimuli apart depends on the overlap between the distributions, quantified by d", the normalized difference between their means. The goal of identifying each stimulus as an example of N or S + N as accurately as possible can be accomplished with a simple decision rule: Establish a criterion value of the decision axis and choose one response for points below it, the other for points above it. The placement of the criterion determines both the hits ("yes" responses to signals) and the false alarms ("yes" responses to noise). If the criterion is high (strict), the observer will make few false alarms, but also not that many hits. By adopting a lower (more lax) criterion (figure 1b), the number of hits is increased, but at the expense of also increasing the false alarm rate. This change in the decision strategy does not affect d", which is therefore a measure of sensitivity that is independent of response bias.

Figure 1 Distributions assumed by SDT to result from N and S + N; the normalized difference between their means is d". Criterion location is strict in (a), lax in (b), but d" is unchanged.

The statistic d" is calculated by assuming that the underlying distributions in the perceptual space are Gaussian and have equal variance. Both of these assumptions can be tested by varying the location of the criterion to construct an ROC (receiver operating characteristic) curve, the hit rate as a function of the false-alarm rate (figure 2). ROCs can be obtained by varying instructions to encourage criterion shifts; or more efficiently by using confidence ratings, interpreting each level of confidence as a different criterion location. Most data are consistent with the assumption of normality (Swets 1986) or the very similar predictions of logistic distributions, which arise from choice theory (Luce 1963). For data sets that reveal unequal variances, accuracy can be measured using the area under the ROC, a statistic that is nonparametric (makes no assumptions about the underlying distributions) when calculated from a full ROC rather than a single hit/false-alarm pair (Macmillan and Creelman 1996).

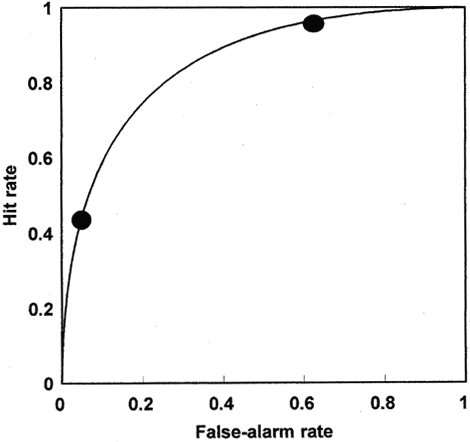
Figure 2 An ROC curve, the relation between hit and false-alarm rates, both of which increase as the criterion location moves (to the left, in figure 1).

The source of the variability in the underlying distributions can be internal or external. When variability is external (as, for example, when a tone is presented in random noise), the statistics of the noise can be used to predict d" for ideal observers (Green and Swets 1966: chap. 6). Similarly, the decision rule adopted by the observer depends on experimental manipulations such as the frequency of the signal, and the optimal criterion location can be predicted using Bayes's rule. Ideal sensitivity and response bias are often not found, but in some detection and discrimination situations they provide a baseline against which observed performance may be measured. The stimulus noise is much harder to characterize in other perceptual situations, such as X-ray reading, where N is healthy tissue and S + N diseased (Swensson and Judy 1981). Most of the many applications of SDT to memory invoke only internal variability. For example, in a recognition memory experiment (Snodgrass and Corwin 1988) the S + N distribution arises from old items and the N items from new ones. Klatzky and Erdelyi (1985) argued that the effect of hypnosis on recognition memory is to alter criterion rather than d", and that distinguishing these possibilities requires presenting both.

The examples so far use a one-interval experimental method for measuring discrimination: in a sequence of trials, N or S + N is presented and the observer attempts to identify the stimulus, with or without a confidence rating. This paradigm has been widely used, but not exclusively: In forced-choice designs, each trial contains m intervals, one with S + N and the rest with N, and the observer chooses the S + N interval; in same-different, two stimuli are presented that may be the same (both S + N or both N) or different (one of each); oddity is like forced-choice, except that the "odd" interval may contain either S + N or both N; and so on. Workers in areas as diverse as SPEECH PERCEPTION and food evaluation have argued that such designs are preferable to the one-interval design in their fields.

In the absence of theory, it is difficult to compare performance across paradigms, but SDT permits the abstraction of the same statistic, d" or a derivative, from all (Macmillan and Creelman 1991). The basis of comparison is that d" can always be construed as a distance measure in a perceptual space that contains multiple distributions. For the one-interval design, this space is one-dimensional, as in figure 1, but for other designs each interval corresponds to a dimension. According to SDT, an unbiased observer with d" = 2 will be correct 93 percent of the time in two-alternative forced-choice but as low as 67 percent in same-different. Some tasks can be approached with more than one decision rule; for example, the optimal strategy in same-different is to make independent observations in the two intervals, whereas in the differencing model the effects of the two intervals are subtracted. By examining ROC curve shapes, Irwin and Francis (1995) concluded that the differencing model was correct for simple visual stimuli, the optimal model for complex ones.

Detection theory also provides a bridge between discrimination and other types of judgment, particularly identification (in which a distinct response is required for each of m stimuli) and classification (in which stimuli are sorted into subclasses). For sets of stimuli that differ along a single dimension, such as sounds differing only in loudness, SDT allows the estimation of d" for each pair of stimuli in both identification and discrimination. The two tasks are roughly equivalent when the range of stimuli is small, but increasingly discrepant as range increases. Durlach and Braida's (1969) theory of resolution describes both types of experiments and relates them quantitatively under the assumption that resolution is limited by both sensory and memory variance, the latter increasing with range.

For more complex stimulus sets, a multidimensional version of SDT is increasingly applied (Graham 1989; Ashby 1992). In natural extensions of the unidimensional model, each stimulus is assumed to give rise to a distribution in a multidimensional perceptual space, distances between stimuli reflect resolution, and the observer uses a decision boundary to divide the space into regions, one for each response. The more complex representation raises new issues about the perceptual interactions between dimensions, and about the form of the decision boundary; many of these concepts have been codified under the rubric of generalized recognition theory, or GRT (Ashby and Townsend 1986). Multidimensional SDT can be used to determine the optimal possible performance, given the MENTAL REPRESENTATION of the observer (Sperling and Dosher 1986). For example, Palmer (1995) accounted for the set-size effect in visual search without assuming any processing limitations, and Graham, Kramer, and Yager (1987) predicted performance in both uncertain detection (in which S + N can take on one of several values) and summation (in which redundant information is available) for several models. In a more complex example of information integration, Sorkin, West, and Robinson (forthcoming) showed how a group decision can be predicted from individual inputs without assumptions about interaction among its members. In all of these cases, as for the complex designs described earlier, SDT provides a baseline analysis of the situation against which data can be compared before specific processing assumptions are invoked.

Additional links

Signal Detection Theory

-- Neil Macmillan

References

Ashby, F. G., Ed. (1992). Multidimensional Models of Perception and Cognition. Hillsdale, NJ: Erlbaum.

Ashby, F. G., and J. T. Townsend. (1986). Varieties of perceptual independence. Psychological Review 93:154-179.

Durlach, N. I., and L. D. Braida. (1969). Intensity perception. 1. Preliminary theory of intensity resolution. Journal of the Acoustical Society of America 46:372-383.

Graham, N., P. Kramer, and D. Yager. (1987). Signal-detection models for multidimensional stimuli: Probability distributions and combination rules. Journal of Mathematical Psychology 31:366-409.

Graham, N. V. (1989). Visual Pattern Analyzers. New York: Oxford University Press.

Green, D. M., and J. A. Swets. (1966). Signal Detection Theory and Psychophysics. New York: Wiley.

Irwin, R. J., and M. A. Francis. (1995). Perception of simple and complex visual stimuli: Decision strategies and hemispheric differences in same-different judgments. Perception 24:787-809.

Klatzky, R. L., and M. H. Erdelyi. (1985). The response criterion problem in tests of hypnosis and memory. International Journal of Clinical and Experimental Hypnosis 33:246-257.

Luce, R. D. (1963). Detection and recognition. In R. D. Luce, R. R. Bush, and E. Galanter, Eds., Handbook of Mathematical Psychology, vol. 1. New York: Wiley, pp. 103-189.

Macmillan, N. A., and C. D. Creelman. (1991). Detection Theory: A User's Guide. New York: Cambridge University Press.

Macmillan, N. A., and C. D. Creelman. (1996). Triangles in ROC space: History and theory of "nonparametric" measures of sensitivity and response bias. Psychonomic Bulletin and Review 3:164-170.

Palmer, J. (1995). Attention in visual search: Distinguishing four causes of a set-size effect. Current Directions in Psychological Science 4:118-123.

Snodgrass, J. G., and J. Corwin. (1988). Pragmatics of measuring recognition memory: Applications to dementia and amnesia. Journal of Experimental Psychology: General 117:34-50.

Sorkin, R. D., R. West, and D. E. Robinson. (Forthcoming). Group performance depends on majority rule. Psychological Science to appear.

Sperling, G. A., and B. A. Dosher. (1986). Strategy and optimization in human information processing. In K. Boff, L. Kaufman, and J. Thomas, Eds., Handbook of Perception and Performance, vol. 1. New York: Wiley, pp. 2-1 to 2 - 65.

Swensson, R. G., and P. F. Judy. (1981). Detection of noisy visual targets: Models for the effects of spatial uncertainty and signal-to-noise ratio. Perception and Psychophysics 29:521-534.

Swets, J. A. (1986). Form of empirical ROCs in discrimination and diagnostic tasks. 99:181-198.

Tanner, W. P., Jr., and J. A. Swets. (1954). A decision-making theory of visual detection. Psychological Review 61:401-409.

Signal Detection Theory

See also

Additional links

References

Further Readings