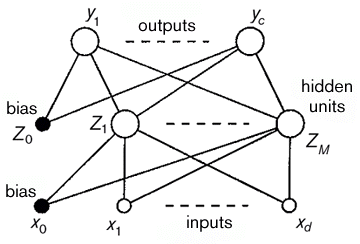
Figure 1 A feed-forward network having two layers of adaptive parameters.
A feedforward network can be viewed as a graphical representation of a parametric function which takes a set of input values and maps them to a corresponding set of output values (Bishop 1995). Figure 1 shows an example of a feedforward network of a kind that is widely used in practical applications.

Figure 1 A feed-forward network having two layers of adaptive parameters.
Vertices in the graph represent either inputs, outputs, or "hidden" variables, while the edges of the graph correspond to the adaptive parameters. We can write down the analytic function corresponding to this network as follows. The output of the jth hidden node is obtained by first forming a weighted linear combination of the d input values xi to give
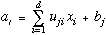
The value of hidden variable j is then obtained by transforming the linear sum in (1) using an activation function g(·) to give
zj = g(aj)
Finally, the outputs of the network are obtained by forming linear combinations of the hidden variables to give
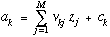
The parameters {uji, vkj} are called weights while {bj, c k} are called biases, and together they constitute the adaptive parameters in the network. There is a one-to-one correspondence between the variables and parameters in the analytic function and the nodes and edges respectively in the graph.
Historically, feedforward networks were introduced as models of biological neural networks (McCulloch and Pitts 1943), in which nodes corresponded to neurons and edges corresponded to synapses, and with an activation function g(a) given by a simple threshold. The recent development of feedforward networks for pattern recognition applications has, however, proceeded largely independently of any biological modeling considerations.
The goal in pattern recognition is to use a set of example solutions to some problem to infer an underlying regularity which can subsequently be used to solve new instances of the problem. Examples include handwritten digit recognition, medical image screening, and fingerprint identification. In the case of feedforward networks, the set of example solutions (called a training set) comprises instances of input values together with corresponding desired output values. The training set is used to define an error function in terms of the discrepancy between the predictions of the network for given inputs and the desired values of the outputs given by the training set. A common example of an error function would be the squared difference between desired and actual output, summed over all outputs and summed over all patterns in the training set. The learning process then involves adjusting the values of the parameters to minimize the value of the error function. Once the network has been trained, that is, once suitable values for the parameters have been determined, new inputs can be applied and the corresponding predictions (i.e., network outputs) calculated.
The use of layered feedforward networks for pattern recognition was widely studied in the 1960s. However, effective learning algorithms were only known for the case of networks in which, at most, one of the layers comprised adaptive interconnections. Such networks were known variously as perceptrons (Rosenblatt 1962) and adalines (Widrow and Lehr 1990), and were seriously limited in their capabilities (Minsky and Papert 1969/1990). Research into artificial NEURAL NETWORKS was stimulated during the 1980s by the development of new algorithms capable of training networks with more than one layer of adaptive parameters (Rumelhart, Hinton, and Williams 1986). A key development involved the replacement of the nondifferentiable threshold activation function by a differentiable nonlinearity, which allows gradient-based optimization algorithms to be applied to the minimization of the error function. The second key step was to note that the derivatives could be calculated in a computationally efficient manner using a technique called backpropagation, so called because it has a graphical interpretation in terms of a propagation of error signals from the output nodes backward through the network. Originally these gradients were used in simple steepest-descent algorithms to minimize the error function. More recently, however, this has given way to the use of more sophisticated algorithms, such as conjugate gradients, borrowed from the field of nonlinear optimization (Gill, Murray, and Wright 1981).
During the late 1980s and early 1990s, research into feedforward networks emphasized their role as function approximators. For example, it was shown that a network consisting of two layers of adaptive parameters could approximate any continuous function from the inputs to the outputs with arbitrary accuracy provided the number of hidden units is sufficiently large and provided the network parameters are set appropriately (Hornik, Stinchcombe, and White 1989). More recently, however, feedforward networks have been studied from the much richer probabilistic perspective (see PROBABILITY, FOUNDATIONS OF), which sets neural networks firmly within the field of statistical pattern recognition (Fukunaga 1990). For instance, the outputs of the network can be given a probabilistic interpretation, and the role of network training is then to model the probability distribution of the target data, conditioned on the input variables. Similarly, the minimization of an error function can be motivated from the well-established principle of maximum likelihood that is widely used in statistics. An important advantage of this probabilistic viewpoint is that it provides a theoretical foundation for the study and application of feedforward networks (see STATISTICAL LEARNING THEORY), as well as motivating the development of new models and new learning algorithms.
A central issue in any pattern recognition application is that of generalization, in other words the performance of the trained model when applied to previously unseen data. It should be emphasized that a small value of the error function for the training data set does not guarantee that future predictions will be similarly accurate. For example, a large network with many parameters may be capable of achieving a small error on the training set, and yet fail to model the underlying distribution of the data and hence achieve poor performance on new data (a phenomenon sometimes called "overfitting"). This problem can be approached by limiting the complexity of the model, thereby forcing it to extract regularities in the data rather than simply memorizing the training set. From a fully probabilistic viewpoint, learning in feedforward networks involves using the network to define a prior distribution over functions, which is converted to a posterior distribution once the training data have been observed. It can be formalized through the framework of BAYESIAN LEARNING, or equivalently through the MINIMUM DESCRIPTION LENGTH approach (MacKay 1992; Neal 1996).
In practical applications of feedforward networks, attention must be paid to the representation used for the data. For example, it is common to perform some kind of preprocessing on the raw input data (perhaps in the form of "feature extraction") before they are used as inputs to the network. Often this preprocessing takes into consideration any prior knowledge we might have about the desired properties of the solution. For instance, in the case of digit recognition we know that the identity of the digit should be invariant to the position of the digit within the input image.
Feedforward neural networks are now well established as an important technique for solving pattern recognition problems, and indeed there are already many commercial applications of feedforward neural networks in routine use.
Anderson, J. A., and E. Rosenfeld, Eds. (1988). Neurocomputing: Foundations of Research. Cambridge, MA: MIT Press.
Bishop, C. M. (1995). Neural Networks for Pattern Recognition. Oxford: Oxford University Press.
Fukunaga, K. (1990). Introduction to Statistical Pattern Recognition. 2nd ed. San Diego: Academic Press.
Gill, P. E., W. Murray, and M. H. Wright. (1981). Practical Optimization. London: Academic Press.
Hornik, K., M. Stinchcombe, and H. White. (1989). Multilayer feedforward networks are universal approximators. Neural Networks 2(5):359-366.
MacKay, D. J. C. (1992). A practical Bayesian framework for back-propagation networks. Neural Computation 4(3):448-472.
McCulloch, W. S., and W. Pitts. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics 5:115-133. Reprinted in Anderson and Rosenfeld (1988).
Minsky, M. L., and S. A. Papert. (1969/1990). Perceptrons. Cambridge, MA: MIT Press.
Neal, R. M. (1996). Bayesian Learning for Neural Networks. Lecture Notes in Statistics 118. Springer.
Rosenblatt, F. (1962). Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Washington, DC: Spartan.
Rumelhart, D. E., G. E. Hinton, and R. J. Williams. (1986). Learning internal representations by error propagation. In D. E. Rumelhart, J. L. McClelland, and the PDP Research Group, Eds., Parallel Distributed Processing: Explorations in the Microstructure of Cognition, vol. 1: Foundations. Cambridge, MA: MIT Press, pp. 318-362. Reprinted in Anderson and Rosenfeld (1988).
Widrow, B., and M. A. Lehr. (1990). 30 years of adaptive neural networks: Perceptron, madeline, and backpropagation. Proceedings of the IEEE 78(9):1415-1442.
Anderson, J. A., A. Pellionisz, and E. Rosenfeld, Eds. (1990). Neurocomputing 2: Directions for Research. Cambridge, MA: MIT Press.
Arbib, M. A. (1987). Brains, Machines, and Mathematics. 2nd ed. New York: Springer-Verlag.
Bishop, C. M. (1994). Neural networks and their applications. Review of Scientific Instruments 65(b):1803-1832.
Bishop, C. M., P. S. Haynes, M. E. U. Smith, T. N. Todd, and D. L. Trotman. (1995). Real-time control of a tokamak plasma using neural networks. Neural Computation 7:206-217.
Block, H. D. (1962). The perceptron: A model for brain functioning. Reviews of Modern Physics 34(1):123-135. Reprinted in Anderson and Rosenfeld (1988).
Broomhead, D. S., and D. Lowe. (1988). Multivariable functional interpolation and adaptive networks. Complex Systems 2:321-355.
Duda, R. O., and P. E. Hart. (1973). Pattern Classification and Scene Analysis. New York: Wiley.
Geman, S., E. Bienenstock, and R. Doursat. (1992). Neural networks and the bias/variance dilemma. Neural Computation 4(1):1-58.
Hertz, J., A. Krogh, and R. G. Palmer. (1991). Introduction to the Theory of Neural Computation. Redwood City, CA: Addison-Wesley.
Jacobs, R. A., M. I. Jordan, S. J. Nowlan, and G. E. Hinton. (1991). Adaptive mixtures of local experts. Neural Computation 3(1):79-87.
Jordan, M. I., and C. M. Bishop. (1997). Neural networks. In A. B. Tucker, Ed., The Computer Science and Engineering Handbook. Boca Raton, FL: CRC Press, pp. 536-556.
Le Cun, Y., B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel. (1989). Backpropagation applied to handwritten zip code recognition. Neural Computation 1(4):541-551.
Lowe, D., and A. R. Webb. (1990). Exploiting prior knowledge in network optimization: An illustration from medical prognosis. Network: Computation in Neural Systems 1(3):299-323.
MacKay, D. J. C. (1995). Bayesian non-linear modelling for the 1993 energy prediction competition. In G. Heidbreder, Ed., Maximum Entropy and Bayesian Methods, Santa Barbara 1993. Dordrecht: Kluwer.
MacKay, D. J. C. (1995). Probable networks and plausible predictions -- a review of practical Bayesian methods for supervised neural networks. Network: Computation in Neural Systems 6(3):469-505.