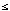P(A|I) 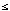1 According to one widely held interpretation of probability, the numerical probability assigned to a proposition given particular evidence is a measure of belief in that proposition given the evidence. For example, the statement "The probability that the next nerve impulse will occur within .1 seconds of the previous impulse is .7, given that 70 of the last 100 impulses occured within .1 seconds" is an assertion of degree of belief about a future event given evidence of previous similar events. In symbols this would be written:
where the "|" symbol (called the "givens") separates the target proposition (on the left) from the evidence used to support it (on the right), the conditioning evidence. It is now widely accepted that unconditioned probability statements are either meaningless or a shorthand for cases where the conditioning information is understood.
Probability can be viewed as a generalization of classical propositional LOGIC that is useful when the truth of particular propositions is uncertain. This generalization has two important components: one is the association of a numerical degree of belief with the proposition; the other is the explicit dependence of that degree of belief on the evidence used to assess it. Writers such as E. T. Cox (1989) and E. T. Jaynes (1998) have derived standard probability theory from this generalization and the requirement that probability should agree with standard propositional logic when the degree of belief is 1 (true beyond doubt) or 0 (false beyond doubt). This means that any entity that assigns degrees of belief to uncertain propositions, given evidence, must use probability to do so, or be subject to inconsistencies, such as assigning different degrees of belief to the same proposition given the same evidence depending on the order that the evidence is evaluated. The resulting laws of probability are:
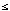P(A|I) 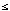1 All other probability laws, such as Bayes's theorem, can be constructed from the above laws.
This derivation of probability provides a neat resolution to the old philosophical problem of justifying INDUCTION. In the eighteenth century, the philosopher David HUME disproved the assumption that all "truth" could be established deductively, as in mathematics, by showing that propositions such as "The sun will rise tomorrow" can never be known with certainty, no matter how may times the sun has risen in the past. That is, generalizations induced from particular evidence are always subject to possible refutation by further evidence. However, an entity using probability will assign such a high probability to the sun rising tomorrow, given the evidence, that it is rational for it to make decisions based on this belief, even in the absence of complete certainty.
Several important consequences follow from this "conditioned degree of belief" interpretation of probability. One consequence is that two different probability assertions, such as the one above, and
are not contradictory because the probabilities involve different conditioning evidence, although the latter assertion is a better predictor if its conditioning evidence is correct. Different entities can condition on different evidence, and so can assign different probability values to the same proposition. This means that there is a degree of subjectivity in evaluating probabilities, because different subjects generally have different experience. However, when different subjects agree on the evidence, they typically give the same probabilities. That is, a degree of objectivity with probabilities can be achieved through intersubjective agreement. Another consequence of the degree of belief interpretation of probability is that the conditioning propositions do not have to be true -- a probability assertion gives the numeric probability assuming the conditioning information is true. This means that probability theory can be used for hypothetical reasoning, such as "If I drop this glass, it will probably break ."
Another consequence of the degree of belief interpretation of probability is that there is no such thing as the probability of a proposition; the numerical degree is always dependent on the conditioning evidence. This means that a statement such as "the probability of a coin landing tails is 1/2," is meaningless -- some experts are able to flip coins on request so that they land heads or tails. The existence of such experts refutes the view that the probability of 1/2 for tails is a physical property of the coin, just like its mass, as has been asserted by some writers. The reason many users of probability talk about "the" probability of tails for a coin or any other event is that the event occurence is assumed to be under "typical" or "normal" conditions. In a "normal" coin toss, we expect tails with a probability of 1/2, but this probability is conditioned on the normality of the toss and the coin, and has no absolute status relative to any other conditional probability about coins. Probabilities that are implicitly conditioned by "normal" operation are called by some "propensities," and assumed to be an intrinsic property of a proposition. For example, an angry patient has a propensity to throw things, even if that patient is physically restrained. However, this statement is just a shorthand for the probability of the patient to behave in a particular way, conditioned on being angry and unconstrained -- "normal" behavior for an angry person.
Although there is universal agreement on the fundamental laws of probability, there is much disagreement on interpretation. The two main interpretations are the "degree of belief" (subjective) interpretation and the "long run frequency" (frequentist or objective) interpretation. In the frequentist interpretation, it is meaningless to assign a probability to a particular proposition, such as "This new type of rocket will launch successfully on the first try," because there are no previous examples on which to base a relative frequency. The degree of belief interpretation can assign a probability in this case by using evidence such as the previous history of other rocket launches, the complexity of the new rocket, the failure rate of machinery of comparable complexity, knowing who built it, and so on. When sufficient frequency evidence is available, and this is the best evidence, then the frequentist and the subjectivist will give essentially the same probability. In other words, when the observed frequency of similar events is used as the conditioning information, both interpretations agree, but the degree of belief interpretation gives reasonable answers even when there is insufficient frequency information.
The main form of probabilistic inference in the degree of belief interpretation is to use Bayes's theorem to go from a prior probability (or just "prior") on a proposition to a posterior probability conditioned on the new evidence. For this reason, the degree of belief interpretation is referred to as Bayesian inference. It dates back to its publication in 1763 in a posthumous paper by the Rev. Thomas Bayes. However, before any specific evidence has been incorporated in Bayesian inference, a prior probability distribution must be given over the propositions of interest. In 1812, Pierre Simon Laplace proposed using the "principle of indifference" to assign these initial (prior) probabilities. This principle gives equal probability to each possibility. When there are constraints on this set of possibilities, the "principle of maximum entropy" (Jaynes 1989) must be used as the appropriate generalization of the principle of indifference. Even here, subjectivity is apparent, as different observers may perceive different sets of possibilities, and so assign different prior probabilities using the principle of indifference. For example, a colorblind observer may see only small and large flowers in a field, and so assign a prior probability of 1/2 to the small size possibility; but another observer sees that the large flowers have two distinct colors, and so assigns a prior probability of 1/3 to the small size possibility because this is now one of three possibilities. There is no inconsistency here, as the different observers have different information. As specific flower data is collected, a better estimate of the small flower probability can be obtained by calculating the posterior probability conditioned on the flower data. If there is a large flower sample, the posterior probabilities for both observers converges to the same value. In other words, data will quickly "swamp" weak prior probabilities such as those based on the principle of indifference, which is why different priors are typically not important in practice.
The main reason for the vehement disagreement between the frequentist (or classical statistics) interpretation and the degree of belief (or Bayesian) interpretation is the perjorative label "subjective" associated with the Bayesian approach, particularly in the assignment of prior probabilities. This dispute is largely academic, as in practice, domain knowledge usually suggests appropriate priors. Because priors are inherently subjective does not mean that they are arbitrary, as they are based on the subject's experience. Recently, writers such as J. O. Berger (1985) have shown that the "objective" frequentist interpretation is just as subjective as the Bayesian. In other words, the attempt to circumscribe the definition of probability to "objective" long-run frequencies not only greatly reduced its applicability but did not succeed in eliminating the inherent subjectivity in reasoning under UNCERTAINTY.
Bayes, T. (1763). An essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society of London 53: pp. 370-418.
Berger, J. O. (1985). Statistical Decision Theory and Bayesian Analysis. 2nd ed. Springer.
Cox, E. T. (1989). Bayesian Statistics: Principles, Models, and Applications. S. James Press, Wiley.
Jaynes, E. T. (1989). Where do we stand on maximum entropy. In R. Rosenkrantz, Ed., E. T. Jaynes: Papers on Probability, Statistics and Statistical Physics. Dordrecht: Kluwer.
Jaynes, E. T. (1998). "Probability Theory: The Logic of Science." Not yet published book available at http://omega.albany.edu: 8008/JaynesBook.html.
Laplace, P. S. (1812). Théorie Analytique des Porbabiletés. Paris: Courcier .
Copyright © 1999 Massachusetts Institute of Technology