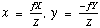
Machine vision is an applied science whose objective is to take two-dimensional (2-D) images as input and extract information about the three-dimensional (3-D) environment adequate for tasks typically performed by humans using vision. These tasks fall into four broad categories:
The most basic fact about vision, whether machine or human, is that images are produced by perspective projection. Consider a coordinate system with origin at the optical center of a camera whose optical axis is aligned along the Z axis. A point P with coordinates (X,Y,Z) in the scene gets imaged at the point P", with image plane coordinates (x,y) where
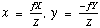
and f is the distance from the optical center of the camera to the image plane. All points in the 3-D world that lie on a ray passing through the optical center are mapped to the same point in the image. During reconstruction, we seek to recover the 3-D information lost during perspective projection.
Many cues are available in the visual stimulus to make this possible, including structure from motion, binocular stereopsis, texture, shading, and contour. Each of these relies on background assumptions about the physical scene (Marr 1982).
The cues of stereopsis and structure from motion rely on the presence of multiple views, either acquired simultaneously from multiple cameras or over time from a single camera during the relative motion of objects. When the projections of a sufficient number of points in the world are observed in multiple images, it is theoretically possible to deduce the 3-D locations of the points as well as of the cameras (Faugeras 1993; for further discussion of the mathematics, see STEREO AND MOTION PERCEPTION).
Shape can be recovered from visual TEXTURE -- a spatially repeating pattern on a surface such as windows on a building, spots on a leopard, or pebbles on a beach. If the arrangement is periodic, or at least statistically regular, it is possible to recover surface orientation and shape from a single image (Malik and Rosenholtz 1997). While the sizes, shapes, and spacings of the texture elements (texels) are roughly uniform in the scene, the projected size, shape, and spacing in the image vary, principally because
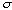 ,
where
,
where 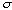 is the angle between the surface
normal and the ray from the viewer.
is the angle between the surface
normal and the ray from the viewer.Expressions can be derived for the rate of change of various image texel features, for example, area, foreshortening, and density (GIBSON"s texture gradients), as functions of surface shape and orientation. One can then estimate the surface shape, slant, and tilt that would give rise to the measured texture gradients.
Shading -- spatial variation in the image brightness -- is determined by the spatial layout of the scene surfaces, their reflectance properties, and the arrangement of light sources. If one neglects interreflections -- the fact that objects are illuminated not just by light sources but also by light reflected from other surfaces in the scene -- then the shading pattern is determined by the orientation of each surface patch with respect to the light sources. For a diffusely reflecting surface, the brightness of the patch varies as the cosine of the angle between the surface normal and the light source direction. A number of techniques have been developed that seek to invert the process -- to recover the surface orientation and shape giving rise to the observed brightness pattern (Horn and Brooks 1989).
Humans can perceive 3-D shape from line drawings, which suggests that useful information can be extracted from the projected image of the contour of an object (Koenderink 1990). It is easiest to do this for objects that belong to parametrized classes of shapes, such as polyhedra or surfaces of revolution, for which the ambiguity resulting from perspective projection can be resolved by considering only those scene configurations that satisfy the constraints appropriate to the particular class of shapes.
Finally, it should be noted that shape and spatial layout are only some of the scene characteristics that humans can infer from images. Surface color, reflectance, and texture are also perceived simultaneously. In machine vision, there has been some work in this direction. For example, attempts have been made to solve the color constancy problem -- to estimate true surface color, given that the apparent color in the image is determined both by the surface color and the spectral distribution of the illuminant.
Visually Guided Control One of the principal uses of vision is to provide information for manipulating objects and guiding locomotion. Consider the use of vision in driving on a freeway. A driver needs to
The lateral and longitudinal control tasks do not require a complete reconstruction of the environment. For instance, lateral control of the car only requires the following information: the position of the car relative to the left and right lane markers, its orientation relative to the lanes, and the curvature of the upcoming road. A feedback control law can be designed using these measurements and taking into account the dynamics of the car. Several research groups (e.g., Dickmanns and Mysliwetz 1992) have demonstrated vision-based automated driving.
For dynamic tasks, it is important that measurements can be integrated over time to yield better estimates -- Kalman filtering provides one formalism. Often the motion of the sensing device is known (perhaps because it has been commanded by the agent) and estimation of relevant scene properties can be made even more robust by exploiting this knowledge.
It is worth noting that even a partial reconstruction of scene information, as suggested above, may not be necessary. Lateral control could be achieved by feedback directly on image (as opposed to scene) measurements. Just steer so that the left and right lane markers are seen by the forward pointing camera in a symmetric position with respect to the center of the image. For the more general task of navigation around obstacles, other variables computable from the optical flow field have been proposed.
Grouping and Tracking Humans have a remarkable ability to organize their perceptual input -- instead of a collection of values associated with individual photoreceptors, we perceive a number of visual groups, usually associated with objects or well-defined parts of objects. This ability is equally important for machine vision. To recognize objects, we must first separate them from their backgrounds. Monitoring and surveillance applications require the ability to detect individual objects, and track them over time. Tracking can be viewed as grouping in the temporal dimension.
Most machine vision techniques for grouping and tracking can be viewed as attempts to construct algorithmic implementations of various grouping factors studied in the context of humans under the rubric of GESTALT PERCEPTION. For instance, the Gestaltists listed similarity as a major grouping factor -- humans readily form groups from parts of an image that are uniform in color, such as a connected red patch, or uniform in texture, such as a plaid region. Computationally, this has motivated edge detection, a technique based on marking boundaries where neighboring pixels have significant differences in brightness or color. If we look for differences in texture descriptors of image patches, suitably defined, we can find texture edges.
Similarity is only one of the factors that can promote grouping. Good continuation suggests linking edge segments that have directions consistent with being part of a smoothly curving extended contour. Relaxation methods and dynamic programming approaches have been proposed to exploit this factor.
Earlier work in machine vision was based primarily on local methods, which make decisions about the presence of boundaries purely on the information in a small neighborhood of an image pixel. Contemporary efforts aim to make use of global information. A number of competing formalisms, such as Markov random fields (Geman and Geman 1984), layer approaches (Wang and Adelson 1994) based on the expectation maximization technique from statistics, and cut techniques drawn from spectral graph theory (Shi and Malik 1997) are being explored. Some of these allow for the combined use of multiple grouping factors such as similarity in brightness as well as common motion.
The temporal grouping problem, visual tracking, lends itself well to the Kalman filtering formalism for dynamic estimation. At each frame, the position of a moving object is estimated by combining measurements from the current time frame with the predicted position from previous data. Generalizations of this idea have also been developed (see Isard and Blake 1996).
Dickmanns, E. D., and B. D. Mysliwetz. (1992). Recursive 3-D road and relative ego-state recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence 14:199-213.
Faugeras, O. (1993). Three-Dimensional Computer Vision: A Geometric Viewpoint. Cambridge, MA: MIT Press.
Geman, S., and D. Geman. (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence 6:721-741.
Horn, B. K. P., and M. J. Brooks. (1989). Shape from Shading. Cambridge, MA: MIT Press.
Isard, M., and A. Blake. (1996). Contour tracking by stochastic propagation of conditional density. In B. Buxton and R. Cipolla, Eds., Proceedings of the Fourth European Conference on Computer Vision. (ECCV 1996), Cambridge. Berlin: Springer, vol. 1, p. 343-356.
Koenderink, J. J. (1990). Solid Shape. Cambridge, MA: MIT Press.
Malik, J., and R. Rosenholtz. (1997). Computing local surface orientation and shape from texture for curved surfaces. International Journal of Computer Vision 23(2):149-168.
Shi, J., and J. Malik. (1997). Normalized cuts and image segmentation. In Proceedings of the 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, pp. 731-737.
Ullman, S. (1996). High-Level Vision: Object Recognition and Visual Cognition. Cambridge, MA: MIT Press.
Wang, J. Y. A., and E. H. Adelson. (1994). Representing moving images with layers. IEEE Transactions on Image Processing 3(5):625-638.
Haralick, R. M., and L. G. Shapiro. (1992). Computer and Robot Vision. 2 vols. Reading, MA: Addison-Wesley.
Horn, B. K. P. (1986). Robot Vision. Cambridge, MA: MIT Press.
Marr, D. (1982). Vision. San Francisco: Freeman.
Nalwa, V. S. (1993). A Guided Tour of Computer Vision. Reading, MA: Addison Wesley.
Trucco, E., and A. Verri. (1998). Introductory Techniques for 3-D Computer Vision. Englewood Cliffs, NJ: Prentice-Hall .