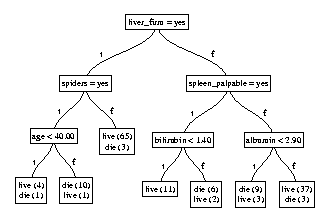
Figure 1
A decision tree is a graphical representation of a procedure for classifying or evaluating an item of interest. For example, given a patient's symptoms, a decision tree could be used to determine the patient's likely diagnosis, or outcome, or recommended treatment. Figure 1 shows a decision tree for forecasting whether a patient will die from hepatitis, based on data from the University of California at Irvine repository (Murphy and Aha 1994). A decision tree represents a function that maps each element of its domain to an element of its range, which is typically a class label or numerical value. At each leaf of a decision tree, one finds an element of the range. At each internal node of the tree, one finds a test that has a small number of possible outcomes. By branching according to the outcome of each test, one arrives at a leaf that contains the class label or numerical value that corresponds to the item in hand. In the figure, each leaf shows the number of examples of each class that fall to that leaf. These leaves are usually not of one class, so one typically chooses the most frequently occurring class label.

A decision tree with a range of discrete (symbolic) class labels is called a classification tree, whereas a decision tree with a range of continuous (numeric) values is called a regression tree. A domain element is called an instance or an example or a case, or sometimes by another name appropriate to the context. An instance is represented as a conjunction of variable values. Each variable has its own domain of possible values, typically discrete or continuous. The space of all possible instances is defined by set of possible instances that one could generate using these variables and their possible values (the cross product).
Decision trees are attractive because they show clearly how to reach a decision, and because they are easy to construct automatically from labeled instances. Two well known programs for constructing decision trees are C4.5 (Quinlan 1993) and CART (Classification and Regression Tree) (Breiman et al. 1984). The tree shown in figure 1 was generated by the ITI (Incremental Tree Inducer) program (Utgoff, Berkman, and Clouse 1997). These programs usually make quick work of training data, constructing a tree in a matter of a few seconds to a few minutes. For those who prefer to see a list of rules, there is a simple conversion, which is available in the C4.5 program. For each leaf of the tree, place its label in the right-hand side of a rule. In the left-hand side, place the conjunction of all the conditions that would need to be true to reach that leaf from the root.
Decision trees are useful for automating decision processes that are part of an application program. For example, for the optical character recognition (OCR) task, one needs to map the optical representation of a symbol to a symbol name. The optical representation might be a grid of pixel values. The tree could attempt to map these pixel values to a symbol name. Alternatively, the designer of the system might include the computation of additional variables, also called features, that make the mapping process simpler. Decision trees are used in a large number of applications, and the number continues to grow as practitioners gain experience in using trees to model decision making processes. Present applications include various pixel classification tasks, language understanding tasks such as pronoun resolution, fault diagnosis, control decisions in search, and numerical function approximation.
A decision tree is typically constructed recursively in a top-down manner (Friedman 1977; Quinlan 1986). If a set of labeled instances is sufficiently pure, then the tree is a leaf, with the assigned label being that of the most frequently occurring class in that set. Otherwise, a test is constructed and placed into an internal node that constitutes the tree so far. The test defines a partition of the instances according to the outcome of the test as applied to each instance. A branch is created for each block of the partition, and for each block, a decision tree is constructed recursively.
One needs to define when a set of instances is to be considered sufficiently pure to constitute a leaf. One choice would be to require absolute purity, meaning that all the instances must be of the same class. Another choice would be to require that the class distribution be significantly lopsided, which is a less stringent form of the complete lopsidedness that one gets when the leaf is pure. This is also known as prepruning because one restricts the growth of the tree before it occurs.
One also needs a method for constructing and selecting a test to place at an internal node. If the test is to be based on just one variable, called a univariate test, then one needs to be able to enumerate possible tests based on that variable. If the variable is discrete, then the possible outcomes could be the possible values of that variable. Alternatively, a test could ask whether the variable has a particular value, making just two possible outcomes, as is the case in figure 1. If the variable is continuous, then some form of discretization needs to be done, so that only a manageable number of outcomes is possible. One can accomplish this by searching for a cutpoint, and then forming a test whether the variable value is less than the cutpoint, as shown in figure 1.
If the test is to be based on more than one variable, called a multivariate test, then one needs to be able to search quickly for a suitable test. This is often done by mapping the discrete variables to continuous variables, and then finding a good linear combination of those variables. A univariate test is also known as an axis-parallel split because in a geometric view of the instance space, the partition formed by a univariate test is parallel to the axes of the other variables. A multivariate test is also known as an oblique split because it need not have any particular characteristic relationship to the axes (Murthy, Kasif, and Salzberg 1994).
One must choose the best test from among those that are allowed at an internal node. This is typically done in a greedy manner by ranking the tests according to a heuristic function, and picking the test that is ranked best. Many heuristic tests have been suggested, and this problem is still being studied. For classification trees, most are based on entropy minimization. By picking a test that maximizes the purity of the blocks, one will probably obtain a smaller tree than otherwise, and researchers and practitioners alike have a longstanding preference for smaller trees. Popular heuristic functions include information gain, gain ratio, GINI, and Kolmogorov-Smirnoff distance. For regression trees, most tests are based on variance minimization. A test that minimizes the variance within the resulting blocks will also tend to produce a smaller tree than one would obtain otherwise.
It is quite possible that a tree will overfit the data. The tree may have more structure than is helpful because it is attempting to produce several purer blocks where one less pure block would result in higher accuracy on unlabeled instances (instance not used in training). This can come about due to inaccurate variable measurements or inaccurate label or value assignments. A host of postpruning methods are available that reduce the size of the tree after it has been grown. A simple method is to set aside some of the training instances, called the pruning set, before building the tree. Then after the tree has been built, do a postorder traversal of the tree, reducing each subtree to a leaf if the proposed leaf would not be significantly less accurate on the pruning set than the subtree it would replace. This issue of balancing the desire for purity with the desire for accuracy is also called the bias-variance trade-off. A smaller tree has higher bias because the partition is coarser, but lower variance because the leaves are each based on more training instances.
During the mid-1990s, researchers developed methods for using ensembles of decision trees to improve accuracy (Dietterich and Bakiri 1995; Kong and Dietterich 1995; Breiman 1996). To the extent that different decision trees for the same task make independent errors, a vote of the set of decision trees can correct the errors of the individual trees.
Breiman, L. (1996). Bagging predictors. Machine Learning 24:123-140.
Breiman, L., J. H. Friedman, R. A. Olshen, and C. J. Stone. (1984). Classification and Regression Trees. Belmont, CA: Wadsworth International Group.
Dietterich, T. G., and G. Bakiri. (1995). Solving multiclass learning problems via error-correcting output codes. Journal of Artificial Intelligence 2:263-286.
Friedman, J. H. (1977). A recursive partitioning decision rule for nonparametric classification. IEEE Transactions on Computers, C-26:404-408.
Kong, E. B., and T. G. Dietterich. (1995). Error-correcting output coding corrects bias and variance. Machine Learning: Proceedings of the Twelfth International Conference. Tahoe City, CA: Morgan Kaufmann, pp. 313-321.
Murphy, P. M., and D. W. Aha. (1994). UCI Repository of Machine Learning Databases. Irvine, CA: University of California, Department of Information and Computer Science.
Murthy, S. K., S. Kasif, and S. Salzberg. (1994). A system for induction of oblique decision trees. Journal of Artificial Intelligence Research 2:1-32.
Quinlan, J. R. (1986). Induction of decision trees. Machine Learning 1:81-106.
Quinlan, J. R. (1993). C4.5: Programs for Machine Learning. San Mateo, CA: Morgan Kaufmann.
Utgoff, P. E., N. C. Berkman, and J. A. Clouse. (1997). Decision tree induction based on efficient tree restructuring. Machine Learning 29:5-44.
Brodley, C. E., and P. E. Utgoff. (1995). Multivariate decision trees. Machine Learning 19:45-77.
Buntine, W., and T. Niblett. (1992). A further comparison of splitting rules for decision-tree induction. Machine Learning 8:75-85.
Chou, P. A. (1991). Optimal partitioning for classification and regression trees. IEEE Transactions on Pattern Analysis and Machine Intelligence 13:340-354.
Draper, B. A., C. E. Brodley, and P. E. Utgoff. (1994). Goal-directed classification using linear machine decision trees. IEEE Transactions on Pattern Analysis and Machine Intelligence 16:888-893.
Jordan, M. I. (1994). A statistical approach to decision tree modeling. Machine Learning: Proceedings of the Eleventh International Conference. New Brunswick, NJ: Morgan Kaufmann, pp. 363-370.
Moret, B. M. E. (1982). Decision trees and diagrams. Computing Surveys 14:593-623.
Murphy, P., and M. Pazzani. (1994). Exploring the decision forest: An empirical investigation of Occam's Razor in decision tree induction. Journal of Artificial Intelligence Research 1:257-275.
Pagallo, G., and D. Haussler. (1990). Boolean feature discovery in empirical learning. Machine Learning 5,1:71-99.
Quinlan, J. R., and R. L. Rivest. (1989). Inferring decision trees using the minimum description length principle. Information and Computation 80:227-248.
Safavian, S. R., and D. Langrebe. (1991). A survey of decision tree classifier methodology. IEEE Transactions on Systems, Man and Cybernetics 21:660-674.
Utgoff, P. E. (1989). Incremental induction of decision trees. Machine Learning 4:161-186.
White, A. P., and W. Z. Liu. (1994). Bias in information-based measures in decision tree induction. Machine Learning 15:321-329.