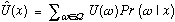Rational Decision Making
Rational
decision making is choosing among alternatives in a way that "properly" accords
with the preferences and beliefs of an individual decision maker
or those of a group making a joint decision. The subject has been
developed in decision theory (Luce and Raiffa 1957; see RATIONAL CHOICE THEORY), decision analysis (Raiffa 1968), GAME THEORY (von Neumann and Morgenstern 1953), political
theory (Muller 1989), psychology (Kahneman, Slovic, and TVERSKY 1982;
see DECISION-MAKING), and economics (Debreu
1959; Henderson and Quandt 1980; see ECONOMICS AND COGNITIVE SCIENCE), in which it is the primary activity of homo
economicus, "rational economic man." The term refers
to a variety of notions, with each conception of alternatives and
proper accord with preferences and beliefs yielding a "rationality" criterion.
At its most abstract, the subject concerns unanalyzed alternatives
(choices, decisions) and preferences reflecting the desirability
of the alternatives and rationality criteria such as maximal desirability of
chosen alternatives with respect to the preference ranking. More
concretely, one views the alternatives as actions in the world,
and determines preferences among alternative actions from preference
rankings of possible states of the world and beliefs or probability
judgments about what states obtain as outcomes of different actions,
as in the maximal expected utility criterion of decision theory
and economics. UTILITY THEORY and the FOUNDATIONS OF PROBABILITY theory provide a base for its developments.
Somewhat unrelated, but common, senses of the term refer to making
decisions through reasoning (Baron 1985), especially reasoning satisfying
conditions of logical consistency and deductive completeness (see DEDUCTIVE REASONING; LOGIC) or probabilistic
soundness (see PROBABILISTIC REASONING). The
basic elements of the theory were set in place by Bernoulli (1738), Bentham
(1823), Pareto (1927), Ramsey (1926), de Finetti (1937), VON NEUMANN and Morgenstern (1953), and Savage (1972). Texts
by Raiffa (1968), Keeney and Raiffa (1976), and Jeffrey (1983) offer
good introductions.
The theory of rational choice begins
by considering a set of alternatives facing the decision maker(s).
Analysts of particular decision situations normally consider only
a restricted set of abstract alternatives that capture the important
or interesting differences among the alternatives. This often proves
necessary because, particularly in problems of what to do, the full range
of possible actions exceeds comprehension. The field of decision
analysis (Raiffa 1968) addresses how to make such modeling choices
and provides useful techniques and guidelines. Recent work on BAYESIAN NETWORKS (Pearl 1988) provides additional modeling techniques.
These models and their associated inference mechanisms form the
basis for a wide variety of successful KNOWLEDGE-BASED SYSTEMS (Wellman, Breese, and Goldman 1992).
The theory next considers a binary
relation of preference among these alternatives. The notation x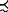 y means that alternative y is
at least as desirable as alternative x, read as y is
weakly preferred to x; "weakly" because x
y means that alternative y is
at least as desirable as alternative x, read as y is
weakly preferred to x; "weakly" because x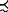 y permits x and y to
be equally desirable. Decision analysis also provides a number of
techniques for assessing or identifying the preferences of decision
makers. Preference assessment may lead to reconsideration of the
model of alternatives when the alternatives aggregate together things
differing along some dimension on which preference depends.
y permits x and y to
be equally desirable. Decision analysis also provides a number of
techniques for assessing or identifying the preferences of decision
makers. Preference assessment may lead to reconsideration of the
model of alternatives when the alternatives aggregate together things
differing along some dimension on which preference depends.
Decision theory requires the weak
preference relation 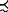 to be a complete
preorder, that is, reflexive (x
to be a complete
preorder, that is, reflexive (x 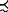 x), transitive
(x
x), transitive
(x 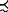 y and y
y and y 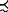 z imply x
z imply x
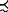 z), and relating every pair of alternatives
(either x
z), and relating every pair of alternatives
(either x 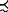 y or y
y or y
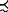 x). These requirements provide a
formalization in accord with ordinary intuitions about simple decision
situations in which one can readily distinguish different amounts,
more is better, and one can always tell which is more. Various theoretical
arguments have also been made in support of these requirements;
for example, if someone's preferences lack these properties,
one may construct a wager against him he is sure to lose.
x). These requirements provide a
formalization in accord with ordinary intuitions about simple decision
situations in which one can readily distinguish different amounts,
more is better, and one can always tell which is more. Various theoretical
arguments have also been made in support of these requirements;
for example, if someone's preferences lack these properties,
one may construct a wager against him he is sure to lose.
Given a complete preordering of alternatives,
decision theory requires choosing maximally desirable alternatives,
that is, alternatives x such that y 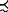 x for all alternatives y. There
may be one, many, or no such maxima. Maximally preferred alternatives
always exist within finite sets of alternatives. Preferences that
linearly order the alternatives ensure that maxima are unique when
they exist.
x for all alternatives y. There
may be one, many, or no such maxima. Maximally preferred alternatives
always exist within finite sets of alternatives. Preferences that
linearly order the alternatives ensure that maxima are unique when
they exist.
The rationality requirements of decision
theory on preferences and choices constitute an ideal rarely observed
but useful nonetheless (see Kahneman, Slovic, and Tversky 1982; DECISION MAKING, ECONOMICS AND COGNITIVE SCIENCE, JUDGMENT HEURISTICS). In practice, people apparently violate reflexivity
(to the extent that they distinguish alternative statements of the
same alternative), transitivity (comparisons based on aggregating
subcomparisons may conflict), and completeness (having to adopt
preferences among things never before considered). Indeed, human
preferences change over time and through reasoning and action, which
renders somewhat moot the usual requirements on instantaneous preferences.
People also seem to not optimize their choices in the required way,
more often seeming to choose alternatives that are not optimal but
are nevertheless good enough. These "satisficing" (Simon
1955), rather than optimizing, decisions constitute a principal
focus in the study of BOUNDED RATIONALITY,
the rationality exhibited by agents of limited abilities (Horvitz
1987; Russell 1991; Simon 1982). Satisficing forms the basis of
much of the study of PROBLEM SOLVING in artificial intelligence;
indeed, NEWELL (1982: 102) identifies the method
of problem solving via goals as the foundational (but weak) rationality
criterion of the field ("If an agent has knowledge that
one of its actions will lead to one of its goals, then the agent
will select that action"). Such "heuristic" rationality
lacks the coherence of the decision-theoretic notion because it
downplays or ignores issues of comparison among alternative actions
that all lead to a desired goal, as well as comparisons among independent
goals. In spite of the failure of humans to live up to the requirements
of ideal rationality, the ideal serves as a useful approximation,
one that supports predictions, in economics and other fields, of
surprisingly wide applicability (Becker 1976; Stigler and Becker 1977).
Though the notions of preference
and optimal choice have qualitative foundations, most practical
treatments of decision theory represent preference orders by means
of numerical utility functions. We say that a function U that assigns
numbers to alternatives represents the relation 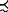 just in case U(x)
just in case U(x)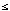 U(y) whenever x
U(y) whenever x 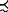 y. Note that if a utility function
represents a preference relation, then any monotone-increasing transform
of the function represents the relation as well, and that such transformation
does not change the set of maximally preferred alternatives. Such
functions are called ordinal utility functions, as the numerical
values only indicate order, not magnitude (so that U(x) = 2
U(y) does not mean that x is twice as desirable as y).
y. Note that if a utility function
represents a preference relation, then any monotone-increasing transform
of the function represents the relation as well, and that such transformation
does not change the set of maximally preferred alternatives. Such
functions are called ordinal utility functions, as the numerical
values only indicate order, not magnitude (so that U(x) = 2
U(y) does not mean that x is twice as desirable as y).
To formalize choosing among actions
that may yield different outcomes with differing likelihoods, the
theory moves beyond maximization of preferability of abstract alternatives
to the criterion of maximizing expected utility, which derives preferences
among alternatives from preference orderings of the possible outcomes
together with beliefs or expectations that indicate the probability
of different consequences. Let 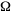 denote the set of possible outcomes
or consequences of choices. The theory supposes that the beliefs
of the agent determine a probability measure Pr, where Pr (
denote the set of possible outcomes
or consequences of choices. The theory supposes that the beliefs
of the agent determine a probability measure Pr, where Pr ( |x)
is the probability that outcome w obtains as a result of taking
action x. The theory further supposes a preference relation
over outcomes. If we choose a numerical function U over
outcomes to represent this preference relation, then the expected
utility Û(x) of alternative x denotes
the total utility of the consequences of x, weighting the
utility of each outcome by its probability, that is
|x)
is the probability that outcome w obtains as a result of taking
action x. The theory further supposes a preference relation
over outcomes. If we choose a numerical function U over
outcomes to represent this preference relation, then the expected
utility Û(x) of alternative x denotes
the total utility of the consequences of x, weighting the
utility of each outcome by its probability, that is
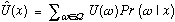
Equation 1
Because the utilities
of outcomes are added together in this definition, this utility
function is called a cardinal utility function, indicating magnitude
as well as order. We then define x 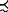 y to hold just
in case Û(x)
y to hold just
in case Û(x) 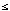 Û(y).
Constructing preferences over actions to represent comparisons of
expected utility in this way transforms the abstract rational choice
criterion into one of maximizing the expected utility of actions.
Û(y).
Constructing preferences over actions to represent comparisons of
expected utility in this way transforms the abstract rational choice
criterion into one of maximizing the expected utility of actions.
The identification of rational choice
under UNCERTAINTY with maximization of expected utility also
admits criticism (Machina 1987). Milnor (1954) examined a number
of reasonable properties one might require of rational decisions,
and proved no decision method satisfied all of them. In practice,
the reasonability of the expected utility criterion depends critically
on whether the modeler has incorporated all aspects of the decision
into the utility function, for example, the decision maker's
attitudes toward risk.
The theory of rational choice may
be developed in axiomatic fashion from the axioms above, in which
philosophical justifications are given for each of the axioms. The
complementary "revealed preference" approach uses
the axioms instead as an analytical tool for interpreting actions.
This approach, pioneered by Ramsey (1926) and de Finetti (1937)
and developed into a useful mathematical and practical method by von
Neumann (von Neumann and Morgenstern 1953) and Savage (1972), uses
real or hypothesized sets of actions (or only observed actions in
the case of Davidson, Suppes, and Siegel 1957) to construct probability
and utility functions that would give rise to the set of actions.
When decisions are to be made by
a group rather than an individual, the above model is applied to
describing both the group members and the group decision. The focus
in group decision making is the process by which the beliefs and
preferences of the group determine the beliefs and preferences of the
group as a whole. Traditional methods for making these determinations,
such as voting, suffer various problems, notably yielding intransitive
group preferences. Arrow (1963) proved that there is no way, in
general, to achieve group preferences satisfying the rationality
criteria except by designating some group member as a "dictator," and using
that member's preferences as those of the group. May (1954), Black
(1963), and others proved good methods exist in a number of special
cases (Sen 1977). When all preferences are well behaved and concern
exchanges of economic goods in markets, the theory of general equilibrium
(Arrow and Hahn 1971; Debreu 1959) proves the existence of optimal
group decisions about allocations of these goods. Game theory considers
more refined rationality criteria appropriate to multiagent settings
in which decision makers interact. Artificial markets (Wellman 1993)
and negotiation techniques based on game theory (Rosenschein and Zlotkin 1994)
now form the basis for a number of techniques in MULTIAGENT SYSTEMS.
-- Jon Doyle
References and Further Readings
Arrow, K. J. (1963). Social Choice and
Individual Values. 2nd ed. New Haven: Yale University Press.
Arrow, K. J., and F. H. Hahn. (1971). General
Competitive Analysis. Amsterdam: Elsevier.
Baron, J. (1985). Rationality and Intelligence. Cambridge:
Cambridge University Press.
Becker, G. S. (1976). The Economic Approach
to Human Behavior. Chicago: University of Chicago Press.
Bentham, J. (1823). Principles of Morals
and Legislation. Oxford: Oxford University Press.
Bernoulli, D. (1738). Specimen theoriae novae
de mensura sortis. Comentarii academiae scientarium imperialis
Petropolitanae, vol. 5 for 1730 and 1731, pp. 175-192.
Black, D. (1963). The Theory of Committees
and Elections. Cambridge: Cambridge University Press.
de Finetti, B. (1937). La prévision: Ses
lois logiques, ses sources subjectives. Annales de l'Institut
Henri Poincaré 7.
Davidson, D., P. Suppes, and S. Siegel. (1957). Decision
Making: An Experimental Approach. Stanford, CA: Stanford
University Press.
Debreu, G. (1959). Theory of Value: An
Axiomatic Analysis of Economic Equlibrium. New York: Wiley.
Henderson, J. M., and R. E. Quandt. (1980). Microeconomic
Theory: A Mathematical Approach. 3rd ed. New York: McGraw-Hill.
Horvitz, E. J. (1987). Reasoning about beliefs
and actions under computational resource constraints. Proceedings
of the Third AAAI Workshop on Uncertainty in Artificial Intelligence. Menlo
Park, CA: AAAI Press.
Jeffrey, R. C. (1983). The Logic of Decision. 2nd
ed. Chicago: University of Chicago Press.
Kahneman, D., P. Slovic, and A. Tversky, Eds.
(1982). Judgment under Uncertainty: Heuristics and Biases. Cambridge:
Cambridge University Press.
Keeney, R. L., and H. Raiffa. (1976). Decisions
with Multiple Objectives: Preferences and Value Tradeoffs. New
York: Wiley.
Luce, R. D., and H. Raiffa. (1957). Games
and Decisions. New York: Wiley.
Machina, M. J. (1987). Choice under uncertainty:
Problems solved and unsolved. Journal of Economic Perspectives 1(1):121-154.
May, K. O. (1954). Intransitivity, utility,
and the aggregation of preference patterns. Econometrica 22:1-13.
Milnor, J. (1954). Games against nature. In
R. M. Thrall, C. H. Coombs, and R. L. Davis, Eds., Decision
Processes. New York: Wiley, pp. 49-59.
Mueller, D. C. (1989). Public Choice 2. 2nd
ed. Cambridge: Cambridge University Press.
Newell, A. (1982). The knowledge level. Artificial
Intelligence 18(1):87-127.
Pareto, V. (1927). Manuel d'economie
politique, deuxième édition. Paris: M. Giard.
Pearl, J. (1988). Probabilistic Reasoning
in Intelligent Systems: Networks of Plausible Inference. San
Mateo, CA: Morgan Kaufmann.
Raiffa, H. (1968). Decision Analysis:
Introductory Lectures on Choices Under Uncertainty. Reading,
MA: Addison-Wesley.
Ramsey, F. P. (1964). Truth and probability.
In H. E. Kyburg, Jr. and H. E. Smokler, Eds., Studies in Subjective
Probability. New York: Wiley. Originally published 1926.
Rosenschein, J. S., and G. Zlotkin. (1994). Rules
of Encounter: Designing Conventions for Automated Negotiation among
Computers. Cambridge, MA: MIT Press.
Russell, S. J. (1991). Do the Right Thing:
Studies in Limited Rationality. Cambridge, MA: MIT Press.
Savage, L. J. (1972). The Foundations
of Statistics. 2nd ed. New York: Dover Publications.
Sen, A. (1977). Social choice theory: A re-examination. Econometrica 45:53-89.
Simon, H. A. (1955). A behavioral model of rational
choice. Quarterly Journal of Economics 69:99-118.
Simon, H. A. (1982). Models of Bounded
Rationality: Behavioral Economics and Business Organization, vol.
2. Cambridge, MA: MIT Press.
Stigler, G. J., and G. S. Becker. (1977). De
gustibus non est disputandum. American Economic Review 67:76-90.
von Neumann, J., and O. Morgenstern. (1953). Theory
of Games and Economic Behavior. 3rd ed. Princeton, NJ: Princeton
University Press.
Wellman, M. P. (1993). A market-oriented programming
environment and its application to distributed multicommodity flow
problems. Journal of Artificial Intelligence Research 1:1-23.
Wellman, M. P., J. S. Breese, and R. P. Goldman.
(1992). From knowledge bases to decision models. The Knowledge
Engineer
ing Review 7(1):35-53.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
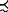 y means that alternative y is
at least as desirable as alternative x, read as y is
weakly preferred to x; "weakly" because x
y means that alternative y is
at least as desirable as alternative x, read as y is
weakly preferred to x; "weakly" because x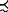 y permits x and y to
be equally desirable. Decision analysis also provides a number of
techniques for assessing or identifying the preferences of decision
makers. Preference assessment may lead to reconsideration of the
model of alternatives when the alternatives aggregate together things
differing along some dimension on which preference depends.
y permits x and y to
be equally desirable. Decision analysis also provides a number of
techniques for assessing or identifying the preferences of decision
makers. Preference assessment may lead to reconsideration of the
model of alternatives when the alternatives aggregate together things
differing along some dimension on which preference depends.
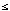 U(y) whenever x
U(y) whenever x 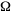 denote the set of possible outcomes
or consequences of choices. The theory supposes that the beliefs
of the agent determine a probability measure Pr, where Pr (
denote the set of possible outcomes
or consequences of choices. The theory supposes that the beliefs
of the agent determine a probability measure Pr, where Pr ( |x)
is the probability that outcome w obtains as a result of taking
action x. The theory further supposes a preference relation
over outcomes. If we choose a numerical function U over
outcomes to represent this preference relation, then the expected
utility Û(x) of alternative x denotes
the total utility of the consequences of x, weighting the
utility of each outcome by its probability, that is
|x)
is the probability that outcome w obtains as a result of taking
action x. The theory further supposes a preference relation
over outcomes. If we choose a numerical function U over
outcomes to represent this preference relation, then the expected
utility Û(x) of alternative x denotes
the total utility of the consequences of x, weighting the
utility of each outcome by its probability, that is