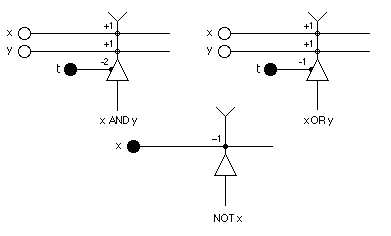
John von Neumann was born in Hungary in 1903 and died in the United States in 1957. He was without doubt one of the great intellects of the century, and one of its most distinguished mathematicians. At the time of his death he was a member of the Institute for Advanced Study, at Princeton, New Jersey.
Von Neumann's scientific interests were very broad, ranging through mathematical logic, automata theory and computer science, pure mathematics -- analysis, algebra and geometry, applied mathematics -- hydrodynamics, meteorology, astrophysics, numerical computation, game theory, quantum and statistical mechanics, and finally to brain mechanisms and information processing. In addition von Neumann was heavily involved in the Manhattan Project both at the University of Chicago and at Los Alamos. After World War II he became a member of the Atomic Energy Commission, and of course he was a key figure in the early U.S. development of general purpose digital computers.
So far as the cognitive sciences are concerned, von Neumann's main contributions were somewhat indirect. Together with Oscar Morgenstern he developed a mathematical model for GAME THEORY that has many implications for human cognitive behavior. He also published two papers and one short monograph on AUTOMATA theory and related topics.
The first paper, published in the 1951 proceedings of the Hixon Symposium, was entitled "The General and Logical Theory of Automata." In it von Neumann introduced what are now known as cellular automata, and discussed in some detail the problem of designing a self-reproducing automaton. In some ways this is a remarkable paper in that it seems to anticipate the mechanism by which information is transmitted from DNA via messenger RNA to the ribosomal machinery underlying protein synthesis in all pro- and eukaryotes. Of more relevance for cognitive science was von Neumann's analysis of the logic of self-reproduction, which he showed to be closely related to Gödel's work on metamathematics and logic (see GÖDEL'S THEOREMS and SELF-ORGANIZING SYSTEMS). His starting point was MCCULLOCH and PITTS's ground-breaking work on the mathematical representation of neurons and neural nets.
The McCulloch-Pitts neuron is an extremely simplified representation of the properties of real neurons. It was introduced in 1943, and was based simply on the existence of a threshold for the activation of a neuron. Let ui(t) denote the state of the ith neuron at time t. Suppose ui = 1 if the neuron is active, 0 otherwise. Let Ø[v] be the Heaviside step function, = 1 if v ≥ 0, 0 if v < 0. Let time be measured in quantal units Δt, so that u(t + Δt) = u(nΔt + Δt) = u(n + 1). Then the activation of a McCulloch-Pitts neuron can be expressed by the equation:
ui(n + 1) = Ø[∑j wij uj(n) - vTH]
where wij is the strength or "weight" of the (j → i)th connection, and where vTH is the voltage threshold. Evidently activation occurs iff the total excitation v = ∑j wij uj(n) - vTH reaches or exceeds 0.
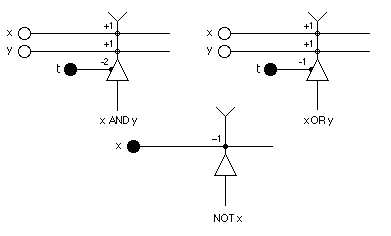
Figure 1. McCulloch-Pitts neurons. Each unit is activated iff its total excitation reaches or exceeds 0. For example, the first unit is activated iff both the units x and y are activated, for only then does the total excitation, (+1)x + (+1)y balance the threshold bias of -2 set by the threshold unit, t, whenever both x and y equal +1 (activated). The t-unit is always active. The numbers (±1), etc. shown above are called "weights." Positive weights denote "excitatory" synapses, negative weights "inhibitory" ones. Similarly, open circles denote excitatory neurons; filled circles, inhibitory ones.
What McCulloch and Pitts discovered was that nets comprising their simplified neural units could represent the logical functions AND, OR, NOT and the quantifiers ∃ and ∀. These elements are sufficient to express most logical and mathematical concepts and formulas. Thus, in von Neumann's words, "anything that you can describe in words can also be done with the neuron method." However von Neumann also cautioned that "it does not follow that there is not a considerable problem left just in saying what you think is to be described." He conjectured that there exists a certain level of complexity associated with an automaton, below which its description and embodiment in terms of McCulloch- Pitts nets is simpler than the original automaton, and above which it is more complicated. He suggested, for example, that "it is absolutely not clear a priori that there is any simpler description of what constitutes a visual analogy than a description of the visual brain." The implications of this work for an understanding of the nature of human perception, language, and cognition have never been analyzed in any detail.
In his second paper, "Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components," published in 1956 (but based on notes taken at a lecture von Neumann gave at CalTech in 1952), von Neumann took up another problem raised by McCulloch, of how to build fault tolerant automata.
Von Neumann solved the reliability problem in two different ways. His first solution was to make use of the error-correcting properties of majority logic elements. Such an element executes the logical function m(a,b,c) = (a AND b) OR (b AND c) OR (c AND a). The procedure is to triplicate each logical function to be executed, that is, execute each logical function three times in parallel, and then feed the outputs through majority logic elements.
Von Neumann's second solution to the reliability problem was to multiplex, that is, use N McCulloch-Pitts circuits to do the job of one. In such nets one bit of information (the choice between "1" and "0") is signaled not by the activation of one neuron, but instead by the synchronous activation of many neurons. Let Δ be a number between 0 and 1. Then "1" is signaled if ξ, the fraction of activated neurons involved in any job, exceeds Δ otherwise "0" is signaled. Evidently a multiplexed net will function reliably only if is close to either 0 or 1. Von Neumann achieved this as follows. Consider nets made up entirely of NAND logic functions, as shown in figure 2.
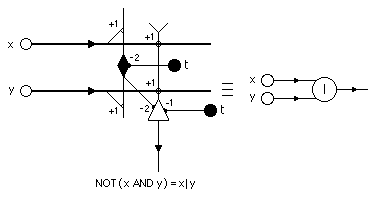
Figure 2. NAND logic function implemented by a McCulloch-Pitts net comprising two units.
Von Neumann subsequently proved that if circuits are built from such elements, then for N large, Δ = 0.07 and the probability of an element malfunctioning, ε < 0.0107, the probability of circuit malfunction can be made to decrease with increasing N. With ε = 0.005, von Neumann showed that for logical computations of large depth the method of multiplexing is superior to majority logic decoding.
McCulloch was aware of the fact that the central nervous system (CNS) seems to function reliably in many cases, even in the presence of brain damage, or of fluctuations in baseline activity. It was therefore natural to look at how neural networks could be designed to achieve such performance. Von Neumann's work triggered a number of efforts to improve on his results, and led directly to the introduction of parallel distributed processing (Winograd and Cowan 1963), and indirectly to work on perceptrons and adalines, and associative memories.
Von Neumann's last publication in this area was the monograph "The Computer and the Brain," published posthumously in 1958, and based on his 1956 manuscript prepared for the Silliman Lectures at Yale University. In this monograph von Neumann outlined his view that computations in the brain are reliable but not precise, statistical and not deterministic, and essentially parallel rather than serial (see also COMPUTATION AND THE BRAIN). Had he lived he would have undoubtedly developed these themes into a detailed theory of brain-like computing. One can see in the many developments in artificial NEURAL NETWORKS since 1957 many echoes of von Neumann's ideas and insights.
McCulloch, W. S., and W. H. Pitts. (1943). A logical calculus of the ideas immanent in nervous activity. Bul. Math. Biophys. 5:115-133.
Von Neumann, J. (1951). The general and logical theory of automata. In L. A. Jeffress, Ed., Cerebral Mechanisms in Behavior -- The Hixon Symposium, September 1948, Pasadena, CA. New York: Wiley, pp. 1-31.
Von Neumann, J. (1956). Probabilistic logics and the synthesis of reliable organisms from unreliable components. In C. E. Shannon and J. McCarthy, Eds., Automata Studies. Princeton: Princeton University Press, pp. 43-98.
Von Neumann, J. (1958). The Computer and the Brain, Silliman Lectures. New Haven, CT: Yale University Press.
Von Neumann, J., and O. Morgenstern. (1944). Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press.
Winograd, S., and J. D. Cowan. (1963). Reliable Computation in the Presence of Noise. Cambridge, MA: MIT Press .