Game Theory
Game theory
is a mathematical framework designed for analyzing the interaction
between several agents whose decisions affect each other. In a game-theoretic
analysis, an interactive situation is described as a game:
an abstract description of the players (agents), the courses of
actions available to them, and their preferences over the possible
outcomes. The game-theoretic framework assumes that the players
employ RATIONAL DECISION MAKING, that is, they
act so as to achieve outcomes that they prefer (VON NEUMANN and Morgenstern
1944). Typically, preferences are modeled using numeric utilities,
and players are assumed to be expected utility maximizers.
Unlike decision making for a single
agent, in the multiagent case this assumption is not enough to define
an "optimal decision," because the agent cannot
unilaterally control the outcome. One of the roles of game theory
is to define notions of "optimal solution" for
different classes of games. These solutions assume that players
reason strategically, basing their decisions on their expectations
regarding the behavior of other players. Typically, players are
assumed to have common knowledge that they are all rational
(see MODAL LOGIC).
A large part of game theory deals
with noncooperative situations, where each player acts independently.
In such a game, a strategy si for
player i specifies the action player i should
take in any state of the game. A solution to the game is
a strategy combination s1,
. . . ,sn satisfying
certain optimality conditions.
Most abstractly, a situation is represented
as a strategic form game, where the possible strategies
for the players are simply enumerated. Each strategy combination
s1, . . . , sn leads to some outcome, whose value
to player i is a payoff ui(s
1, . . . , sn). A two-player strategic form game
is often represented by a matrix where the rows are player 1 strategies,
the columns are player 2 strategies, and the matrix entries are
the associated payoff pairs.
The simplest game is a two-player zero-sum game, where the
players' interests are completely opposed (see figure 1). Because any
gain for one player corresponds to a loss for the other, each player
should make a worst-case assumption about the behavior of the
other. Thus, it appears that player 1 should choose the
maximin strategy that achieves 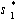 that achieves
that achieves
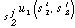 ;
player 2 has an analogous rational strategy
;
player 2 has an analogous rational strategy 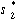 . Common knowledge of
rationality implies that the "rational" strategy of one player will be
known to the other. However,
. Common knowledge of
rationality implies that the "rational" strategy of one player will be
known to the other. However, 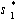 may not be optimal against
may not be optimal against
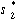 ,
making it irrational for player 1 to play as anticipated. This
circularity can be avoided if we allow the players to use
randomness. In game (a), player 2 can play the mixed strategy
,
making it irrational for player 1 to play as anticipated. This
circularity can be avoided if we allow the players to use
randomness. In game (a), player 2 can play the mixed strategy
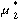 where he chooses heads and tails each with probability
1/2. If each player plays the maximin mixed strategy
where he chooses heads and tails each with probability
1/2. If each player plays the maximin mixed strategy
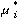 ,
we avoid the problem:
,
we avoid the problem: 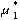 and
and 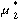 are in
equilibrium, that is, each is optimal against the other (von Neumann
and Morgenstern 1944).
are in
equilibrium, that is, each is optimal against the other (von Neumann
and Morgenstern 1944).
The equilibrium concept can be extended to general n-player
games. A strategy combination 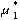 ...
... 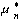 is said to
be in Nash equilibrium (Nash 1950) if no player i
can benefit by deviating from it (playing a strategy
is said to
be in Nash equilibrium (Nash 1950) if no player i
can benefit by deviating from it (playing a strategy 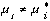 ). In game
(b), the (unique) equilibrium is the nonrandomized strategy
combination (confess, confess). An equilibrium in mixed strategies is
always guaranteed to exist.
). In game
(b), the (unique) equilibrium is the nonrandomized strategy
combination (confess, confess). An equilibrium in mixed strategies is
always guaranteed to exist.
The Nash equilibrium is arguably
the most fundamental concept in noncooperative games. However, several
problems reduce its intuitive appeal. Many games have several very
different equilibria. In such games, it is not clear which equilibrium
should be the "recommended solution," nor how
the players can pick a single equilibrium without communication.
One important mechanism that addresses these concerns is based on
the assumption that the game is played repeatedly, allowing players
to adapt their strategies gradually over time (Luce and Raiffa 1957; Battigalli, Gilli,
and Milinari 1992). This process is a variant of multiagent REINFORCEMENT LEARNING. Some variants are related to BAYESIAN LEARNING (Milgrom and Roberts 1989). Others are related
to the evolution of biological populations, and have led to a branch
of game theory called evolutionary games (Maynard Smith 1982).
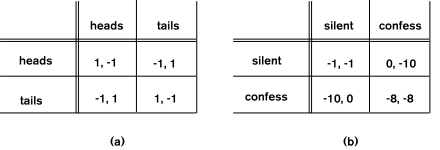
Figure 1
(a) Flipping Pennies. (b) Prisoner's Dilemma: Two conspirators, in
prison, are each given the opportunity to confess in return for a
reduced prison sentence; the payoffs correspond to numbers of years in
prison.
Furthermore, many equilibria are unintuitive. In game (b), the Nash
equilibrium has a utility of -8, -8, which is worse for both
players than the "desired" outcome -1, -1. There have
been many attempts to find alternative models where the desired
outcome is the solution. Some success has been achieved in the case of
infinitely repeated play where the players have BOUNDED RATIONALITY (e.g., when their strategies
are restricted to be finite-state AUTOMATA;
Abreu and Rubenstein 1992).
A more refined representation of
a game takes into consideration the evolution of the game. A game
in extensive form (Kuhn 1953) is a tree whose edges represent
possible actions and whose leaves represent outcomes. Most simply, the
players have perfect information -- any action taken
is revealed to all players.
The notion of equilibrium often leads
to unintuitive results when applied to extensive-form games. For
example, in game (a), the strategy combination (R, a) is
one equilibrium: given that player 2 will play a, player 1
prefers R, and given that player 1 plays R, player
2's choice is irrelevant. This equilibrium is sustained
only by a noncredible "threat" by player 2 to
play the suboptimal move a. The extensive-form equilibrium
concept has been refined to deal with this issue, by adding the
requirement that, at each point in the game, the player's
chosen action be optimal (Selten 1965). In our example, the optimal
move for player 2 is b, and therefore player 1's
optimal action is L. This process, whereby optimal moves
are selected at the bottom of the tree, and these determine optimal
moves higher up, is called backward induction. In the context
of zero-sum games, the algorithm is called the minimax algorithm, and
is the fundamental technique used in GAME-PLAYING SYSTEMS.
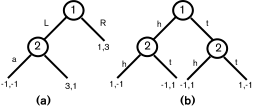
Figure 2
(a) Unintuitive equilibrium. (b) Flipping Pennies.
The extensive
form also includes imperfect information games (Kuhn 1953): the tree
is augmented with information sets, representing sets of
nodes among which the player cannot distinguish. For example, a
simultaneous-move game such as Flipping Pennies can be represented as
in figure (2). Clearly, imperfect information games require the use of
randomization in order to guarantee the existence of a Nash
equilibrium. Refinements of the Nash equilibrium concept addressing
the temporal sequencing of decisions have also been proposed for
imperfect information games (Kreps and Wilson 1982; Selten 1975;
Fudenberg and Tirole 1991), largely based on the intuition that the
player's actions must be optimal relative to his or her
beliefs about the current state.
Game theory also deals with cooperative games,
where players can form coalitions and make binding agreements about
their choice of actions (von Neumann and Morgenstern 1944; Luce
and Raiffa 1957; Shapley and Shubik 1953). In this case, the outcome
of the game is determined by the coalition that forms and the joint
action it takes. The game-theoretic models for such situations typically
focus on how the payoff resulting from the optimal group action
is divided between group members. Various solution concepts have
been proposed for coalition games, essentially requiring that the
payoff division be such that no subgroup is better off by leaving
the coalition and forming another (see Aumann 1989 for a survey).
Game theory is a unified theory for
rational decision making in multiagent settings. It encompasses
bargaining, negotiation, auctions, voting, deterrence, competition,
and more. It lies at the heart of much of economic theory, but it
has also been used in political science, government policy, law,
military analysis, and biology (Aumann and Hart 1992, 1994, 1997). One
of the most exciting prospects for the future is the wide-scale
application of game theory in the domain of autonomous computer
agents (Rosenschein and Zlotkin 1994; Koller and Pfeffer 1997).
See also
Additional links
-- Daphne Koller
References
Abreu, D., and A. Rubinstein. (1992). The structure
of Nash equilibria in repeated games with finite automata. Econometrica 56:1259-1281.
Aumann, R. J., and S. Hart, Eds. (1992; 1994;
1997). Handbook of Game Theory with Economic Applications, vols.
1-3. Amsterdam: Elsevier.
Aumann, R. J. (1976). Agreeing to disagree. Annals
of Statistics 4(6):1236-1239.
Aumann, R. J. (1989). Lectures on Game
Theory. Boulder, CO: Westview Press.
Battigalli, P., M. Gilli, and M. C. Milinari.
(1992). Learning and convergence to equilibrium in repeated strategic
interactions: An introductory survey. Ricerche Economiche 46:335-377.
Fudenberg, D., and J. Tirole. (1991). Perfect
Bayesian equilibrium and sequential equilibrium. Journal of
Economic Theory 53:236-260.
Koller, D., and A. Pfeffer. (1997). Representations
and solutions for game-theoretic problems. Artificial Intelligence.
Kreps, D. M., and R. B. Wilson. (1982). Sequential
equilibria. Econometrica 50:863-894.
Kuhn, H. W. (1953). Extensive games and the
problem of information. In H. W. Kuhn and A. W. Tucker, Eds., Contributions
to the Theory of Games II. Princeton: Princeton University
Press, pp. 193-216.
Luce, R. D., and H. Raiffa. (1957). Games
and Decisions -- Introduction and Critical Survey. New
York: Wiley.
Maynard Smith, J. (1982). Evolution and
the Theory of Games. Cambridge: Cambridge University Press.
Milgrom, P., and J. Roberts. (1989). Adaptive
and Sophisticated Learning in Repeated Normal Forms. Mimeo,
Stanford University.
Nash, J. F. (1950). Equilibrium points in n-person
games. Proceedings of the National Academy of Sciences 36:48-49.
Nash, J. F. (1951). Non-cooperative games. Annals
of Mathematics 54:286-295.
Rosenschein, J. S., and G. Zlotkin. (1994).
Consenting agents: designing conventions for automated negotiation. AI
Magazine 15(3):29-46.
Selten, R. (1965). Spieltheoretische behandlung
eines oligopolmodells mit nachfragetragheit. Zeitschrift
für die gesamte Staatswissenschaft 121:301-324.
Selten, R. (1975). Reexamination of the perfectness
concept for equilibrium points in extensive games. International
Journal of Game Theory 4:25-55.
Shapley, L. S., and M. Shubik. (1953). Solutions
of n-person games with ordinal utilities. Econometrica 21:348-349.
von Neumann, J., and O. Morgenstern. (1944). Theory
of Games and Economic Behavior. Princeton: Princeton University Press.
Further Readings
Aumann, R. J. (1985). What is game theory trying
to accomplish? In K. J. Arrow and S. Honkapohja, Eds., Frontiers
of Economics. Oxford: Blackwell, pp. 28-76.
Aumann, R. J. (1987). Game theory. In J. Eatwell,
M. Milgate, and P. Newman, Eds., The New Palgrave, vol.
2. New York: Macmillan, pp. 460-482.
Fudenberg, D., and J. Tirole. (1991). Game
Theory. Cambridge, MA: MIT Press.
Fudenberg, D. (1992). Explaining cooperation
and commitment in repeated games. In J.-J. Laffont, Ed.,
Advances in Economic Theory, vol. 1. Cambridge:
Cambridge University Press.
Kreps, D. M. (1990). Game Theory and Economic
Modelling. Oxford: Clarendon Press.
McKelvey, R. D., and A. McLennan. (1996). Computation
of equilibria in finite games. In H. Amman, D. Kendrick, and J.
Rust, Eds., Handbook of Computational Economics, vol.
1. Amsterdam: Elsevier.
Megiddo, N., Ed. (1994). Essays in Game
Theory. New York: Springer.
Myerson, R. B., Ed. (1991). Game Theory. Cambridge,
MA: Harvard University Press.
Osborne, M. J., and A. Rubinstein. (1994). A
Course in Game Theory. Cambridge, MA: MIT Press.
Van Damme, E. (1991). Stability and Perfection
of Nash Equilibria. Berlin: Springer.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
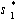 that achieves
that achieves
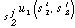 ;
player 2 has an analogous rational strategy
;
player 2 has an analogous rational strategy 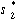 . Common knowledge of
rationality implies that the "rational" strategy of one player will be
known to the other. However,
. Common knowledge of
rationality implies that the "rational" strategy of one player will be
known to the other. However, 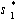 may not be optimal against
may not be optimal against
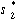 ,
making it irrational for player 1 to play as anticipated. This
circularity can be avoided if we allow the players to use
randomness. In game (a), player 2 can play the mixed strategy
,
making it irrational for player 1 to play as anticipated. This
circularity can be avoided if we allow the players to use
randomness. In game (a), player 2 can play the mixed strategy
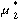 where he chooses heads and tails each with probability
1/2. If each player plays the maximin mixed strategy
where he chooses heads and tails each with probability
1/2. If each player plays the maximin mixed strategy
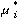 ,
we avoid the problem:
,
we avoid the problem: 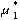 and
and 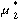 are in
equilibrium, that is, each is optimal against the other (von Neumann
and Morgenstern 1944).
are in
equilibrium, that is, each is optimal against the other (von Neumann
and Morgenstern 1944).
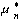 is said to
be in Nash equilibrium (Nash 1950) if no player i
can benefit by deviating from it (playing a strategy
is said to
be in Nash equilibrium (Nash 1950) if no player i
can benefit by deviating from it (playing a strategy 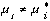 ). In game
(b), the (unique) equilibrium is the nonrandomized strategy
combination (confess, confess). An equilibrium in mixed strategies is
always guaranteed to exist.
). In game
(b), the (unique) equilibrium is the nonrandomized strategy
combination (confess, confess). An equilibrium in mixed strategies is
always guaranteed to exist.

