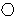,
always 
, eventually 
, and until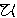 
. For
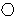example, the formula p ⊃ q means that whenever
p holds, then q must hold in the next state.
Temporal reasoning problems arise in many areas of artificial intelligence (AI), including planning, reasoning about physical systems, discourse analysis, and analysis of time-dependent data. Work in temporal reasoning can be classified in three general categories: algebraic systems, temporal logics, and logics of action. Although useful for many practical tasks, there is little evidence that any of these approaches accurately model human cognition about time. Less formal but more psychologically grounded approaches are discussed in some of the work in AI on plan recognition (Schmidt, Sridhaven, and Goodson 1978), work in linguistics on SEMANTICS and TENSE AND ASPECT (Jackendoff 1983), and the vast psychological literature on MEMORY.
Algebraic systems concentrate on the relationships between time points and/or time intervals, which are represented by named variables. A set of either quantitative or qualitative equations constrain the values that could be assigned to the temporal variables. These equations could take the form of a constraint satisfaction problem (CSP), a set of linear equations, or even a set of assertions in a restricted subset of first-order logic. The goal of the reasoning problem may be to determine consistency, to find a minimal labeling of the CSP, or to find consistent bindings for all the variables over some set of mathematical objects. In all of the algebraic systems described below, time itself is modeled as a continuous linear structure, although there has also been some investigation of discrete linear-time models (Dechter, Meiri, and Pearl 1991) and branching-time models (Ladkin, Angerm, and Rodriguez 1990).
The qualitative temporal algebra, originally devised by Allen (1983) and formalized as an algebra by Ladkin and Maddux (1994), takes time intervals to be primitive. There are thirteen primitive possible relationships between a pair of intervals: for example, before (<) meets (m) (the end of the first corresponds to the beginning of the second), overlaps (o), and so on. These primitive relationships can be combined to form 213 complex relationships. For example, the constraint I1 (< m >) I2 means that I1 is either before, meets, or is after I2. Allen showed how a set of such constraints could be represented by a CSP, and how path-consistency could be used as an incomplete algorithm for computing a minimal set of constraints. The general problem of determining consistency is NP-complete (Vilain, Kautz, and van Beek 1989).
Quantitative algebras allow one to reason about durations of intervals and other metric information. The simple temporal constraint problems (STCSP) of Dechter, Meiri, and Pearl (1991) are a restricted form of linear equations. A time interval I is identified with the pair of its starting point Is and ending point Ie. Difference equations allow one to place constraints on the relative ordering of points. For example, Ie - Js ∈ [-∞, 0] means that I is before J, and Is - Ie ∈ [3, 5] means that the duration of I is between 3 and 5 units. Because they are just linear programs, STCSPs can be solved in polynomial time. General TCSPs allow the right-hand side of an equation to be a union of intervals, rather than a single interval, and solving them is NP-complete. However, TCSPs still cannot express certain complex constraints, such as that two intervals are disjoint but unordered (I (< >) J), which would involve four points (Ie < Js V Je < Is).
Many researchers have explored tractable subsets of these algebras. A subset is specified by the form of the constraints allowed in the statement of the problem instance. Vilain, Kautz, and van Beek (1989) noted that the subset of Allen's algebra that can be exactly translated into equalities and inequalities over start and end points is polynomial. Nebel and Bürckert (1995) generalized this to relations that can be translated into "ord-Horn constraints," the largest tractable subclass that includes all the primitive relations. Koubarakis (1996) and Jonsson and Bäckström (1996) further showed that tractablity still holds if such constraints contain linear combinations of variables. However, none of these classes can express interval disjointed (< >), and in fact any tractable class that includes disjointedness cannot contain all of the primitive relations. Tractable classes including interval disjointedness include some of the "chordal graph" classes of Golumbic and Shamir (1993) and two of the algebras described in Drakengren and Jonsson (1997).
Temporal algebras say nothing about how time intervals or points are associated with events or propositions. In practice, some external mechanism (such as a planning system) generates interval and point tokens that are used to timestamp or index statements in a knowledge base. This external mechanism then computes some of the constraints between the temporal tokens that must hold according to the semantics of the knowledge base (for example, that a token associated with a proposition is disjoint from one associated with the negation of that proposition), and then asks the algebraic reasoning engine to compute consequences of those assertions.
By contrast, temporal logics (van Benthem 1983; Thayse 1989) directly
represent the temporal relationships between propositions, and do away
with any explicit tokens to represent time points or intervals. These
are modal logics, which extend propositional or first-order logic with
temporal operators. For example, propositional linear time temporal
logic models time as a discrete sequence of states, and adds the modal
operators next ,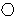
always , eventually , and until 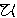. For
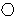example, the formula p ⊃ q means that whenever
p holds, then q must hold in the next state.
The most successful applications of temporal logics have been in the area of program verification (Emerson 1990). One approach to this task exploits the fact that any formula in linear temporal logic can be converted into a kind of finite automata called a Büchi automata. The input language to the automata is sequences of states. The automata accepts exactly those sequences that are models of the corresponding temporal logic formula. In this application, the program to be verified is written as a finite automata, and properties one wishes to verify are written as formulas in temporal logic. The negation of the temporal logic formula is then converted to a Büchi automata, which is then intersected with the program automata. It is then easy to check whether the combined automata accepts any inputs; if it does not, then the program satisfies the desired properties. The worst-case complexity of this procedure is high, because the automata may be exponentially larger than the formula.
Although temporal logics are frequently used in the verification and temporal database communities, they are just beginning to find widespread use in AI, particularly in PLANNING. Applications include the specification and verification of real-time, reactive planners (Rosenschein and Kaelbling 1995; Williams and Nayak 1997), and specification of temporal-extended goals and search control rules (Bacchus and Kabanza 1996).
Finally, temporal reasoning is implicitly performed by all systems used to represent and reason about action and change, such as the SITUATION CALCULUS (McCarthy and Hayes 1969) or dynamic logic (Harel 1979). The situation calculus is simply a style of using first-order logic, in which the final argument to a predicate represents the state in which it holds. Actions are functions from state to state. Thus, the semantics for the situation calculus is based on a discrete, forward-branching model of time. The general approach can also be used to model continuous branching time (Reiter 1996). Successful planning systems have also been built (Blum and Furst 1995; Kautz and Selman 1996) that use a discrete linear model of time, where states are simply natural numbers used to index time-varying predicates.
Allen, J. (1983). Maintaining knowledge about temporal intervals. Comm. ACM 26(11):832-843.
Bacchus, F., and F. Kabanza. (1996). Planning for temporally extended goals. Proc. AAAI-96 Portland, OR.
van Benthem, J. (1983). The Logic of Time. Dordrecht: Reidel.
Blum, A., and M. Furst. (1995). Fast planning through planning graph analysis. Proc. IJCAI-95 Montreal, Canada.
Dechter, R., I. Meiri, and J. Pearl. (1991). Temporal constraint networks. Artificial Intelligence 49:61-95.
Drakengren, T., and P. Jonsson. (1997). Towards a complete classification of tractablility in Allen's algebra. Proc. IJCAI-97 Nagoya, Japan.
Emerson, E. A. (1990). Temporal and modal logic. In J. van Leeuwen, Ed., Handbook of Theoretical Computer Science, vol. B. Elsevier.
Golumbic, M., and R. Shamir. (1993). Complexity and algorithms for reasoning about time: A graph-theoretic approach. J. ACM 40(5):1108-1133.
Harel, D. (1979). First-order dynamic logic. Lecture Notes in Computer Science, vol. 68. Berlin: Springer.
Jackendoff, R. (1983). Semantics and Cognition. Cambridge, MA: MIT Press.
Jonsson, P., and C. Bäckström. (1996). A linear-programming approach to temporal reasoning. Proc. AAAI-96 Portland, OR.
Kautz, H., and B. Selman. (1996). Pushing the envelope: Planning, propositional logic, and stochastic search. Proc. AAAI-96 Portland, OR.
Koubarakis, M. (1996). Tractable disjunctions of linear constraints. Proc. Constraint Logic Programming (CLP-96) Boston, MA.
Ladkin, P., F. Anger, and R. Rodriguez. (1990). Temporal reasoning with intervals in branching time. TR-90028 International Computer Science Institute.
Ladkin, P., and Maddux, R. (1994). On binary constraint problems. J. ACM 41(3):435-469.
McCarthy, J., and P. Hayes. (1969). Some philosophical problems from the standpoint of artificial intelligence. Machine Intelligence 4. Chichester: Ellis Horwood.
Nebel, B., and H. Bürkert. (1995). Reasoning about temporal relations: A maximal tractable subclass of Allen's interval algebra. J. ACM 42(1):43-66.
Reiter, R. (1996). Natural actions, concurrency and continuous time in the situation calculus. Proc. KR-96 Boston, MA.
Rosenschein, S., and L. Kaelbling. (1995). A situated view of representation and control. Artificial Intelligence 73(1):149-174.
Schmidt, C. F., N. S. Sridharan, and J. L. Goodson. (1978). The plan recogition problem: An intersection of psychology and artificial intelligence. Artificial Intelligence 11:45-83.
Thayse, A., Ed. (1989). From Modal Logic to Deductive Databases. Chichester: Wiley.
Vilain, M., H. Kautz, and P. van Beek. (1989). Constraint propagation algorithms for temporal reasoning: A revised report. In J. deKleer and D. Weld, Eds., Readings in Qualitative Reasoning About Physical Systems. Los Altos, CA: Kaufmann.
Williams, B., and P. Nayak. (1997). A reactive planner for a model-based executive. Proc. IJCAI-97 Nagoya, Japan.
Copyright © 1999 Massachusetts Institute of Technology