Supervised Learning in Multilayer Neural Networks
Neural networks
consist of simple processing units that interact via weighted connections.
They are sometimes implemented in hardware but most research involves
software simulations. They were originally inspired by ideas about
how the brain computes, and understanding biological computation
is still the major goal of many researchers in the field (Churchland and Sejnowski
1992). However, some biologically unrealistic neural networks are
both computationally interesting and technologically useful (Bishop 1995).
A typical processing unit first computes
a "total input," which is a weighted sum of the
incoming activities from other units plus a bias. It then puts its
total input through an activation function to determine the activity
of the unit. The most common activation function is the logistic, y = 1/1 + exp(- x).
For deterministic analog units the activity that is communicated
to other units is simply y. For binary stochastic units, y determines
the probability that the activity of the unit is 1 rather than 0.
For binary threshold units, the activity is 1 if the total input
is positive and 0 otherwise. Sensory input to the network is typically
handled by fixing the activities of some "input" units.
The most interesting property of NEURAL NETWORKS is their ability to learn from examples by adapting
the weights on the connections. The most widely used learning algorithms
are supervised: they assume that there is a set of training cases,
each consisting of an input vector and a desired output or output
vector. Learning involves sweeping through the training set many
times, gradually adjusting the weights so that the actual output
produced by the network gets closer to the desired output. The simplest
neural network architecture consists of some input units with directed,
weighted connections to an output unit. Such networks were extensively
studied in the 1960s because there are very simple learning algorithms
that are guaranteed to find the optimal weights when the output
unit uses a linear or binary threshold activation function (Widrow
and Hoff 1960; Rosenblatt 1962). Unfortunately, such simple networks
can only compute a very limited class of functions (Minsky and Papert 1969).
They cannot, for example, compute the exclusive- or of two
binary inputs.
The limitations of simple networks
can be overcome by adding one or more intermediate, "hidden" layers
of nonlinear units between the input and the output. The architecture
remains feedforward, with each unit only receiving inputs from units in
lower layers. With enough hidden units in a single layer, there
exist weights that approximate arbitrarily closely any continuous,
differentiable mapping from a compact input space to a compact output
space. Finding the optimal weights is generally intractable, but
gradient methods can be used to find sets of weights that work well
for many practical tasks. Provided the hidden units use a nonlinearity
with a well-behaved derivative, an algorithm called "backpropagation" (Rumelhart, Hinton,
and Williams 1986) can be used to compute the derivatives, with
respect to each weight in the network, of the error function. The
standard error function is the squared difference between the actual
and desired outputs, but cross-entropy error functions are more
appropriate when the outputs represent class probabilities.
For each training case, the activities
of the units are computed by a forward pass through the network.
Then, starting with the output units, a backward pass through the
network is used to compute the derivatives of the error function
with respect to the total input received by each unit. This computation
is a straightforward application of the chain rule and is as efficient
as the forward pass. Given these derivatives, it is easy to compute
the derivatives of the error function with respect to the weights.
There are many different ways of
using the derivatives computed by backpropagation. In "on-line" learning,
the weights are adjusted after each training case in proportion
to the derivatives for that case. In "batch" learning,
the derivatives are accumulated over the whole training set and
then the weights are adjusted in the direction of steepest descent
in the error function, or in some more sensible direction computed
by a technique such as momentum, conjugate gradients, or delta-bar-delta.
The simple on-line method is the most efficient for very large training
sets in which the data are highly redundant, but batch conjugate
gradient is faster and easier to use for small training sets. There
are also constructive methods that add hidden units one at a time
while keeping the incoming weights of earlier hidden units frozen (Fahlman
and Lebiere 1990).
Feedforward neural networks that
have one or more layers of logistic hidden units and are trained
using backpropagation have worked very well for tasks such as discrimi-nating
similar phonemes (Lang, Waibel, and Hinton 1990) or recognizing handwritten
digits (Le Cun et al. 1989; see also PATTERN RECOGNITION AND FEEDFORWARD NETWORKS). Performance is significantly improved
if natural symmetries of the task are imposed on the network by
forcing different weights to have the same values.
When training data are limited, a
complicated network with a large number of weights is liable to overfit:
it performs very well on the training data, but much less well on
test data drawn from the same distribution. On the other hand, a
simple network with few weights may perform poorly on both training
and test data because it is unable to approximate the true function (Geman, Bienenstock,
and Doursat 1992). Many different methods have been developed for
optimizing the complexity of the network. If part of the training
data is held out as a validation set, it is possible to try different
numbers of hidden units and to pick the number that gives best performance
on the validation set. The "early stopping" method, which
is appropriate when computational resources are limited, stops the
training of a complicated network as soon as its performance on
the validation set starts to deteriorate. Another way of limiting
the complexity of a network is to add a penalty to the error term.
The simplest such penalty is the sum of the squares of the weights
times a penalty coefficient, 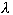 . This
can be viewed in Bayesian terms as a zero-mean Gaussian prior which
favors networks that have small weights.
. This
can be viewed in Bayesian terms as a zero-mean Gaussian prior which
favors networks that have small weights. 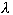 can
be chosen using a validation set but this wastes training data and
is awkward if different values of
can
be chosen using a validation set but this wastes training data and
is awkward if different values of 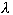 are
required for the input-to-hidden and hidden-to-output weights. MacKay (1995)
has developed Bayesian methods that estimate an appropriate
are
required for the input-to-hidden and hidden-to-output weights. MacKay (1995)
has developed Bayesian methods that estimate an appropriate
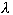 without using a validation set.
without using a validation set.
Performance can almost always be
improved by averaging the outputs of many different networks each
of which overfits the data. Finding the appropriate weights to use
when averaging the outputs can be viewed as a separate learning
task (Wolpert 1992). The benefits of averaging increase as the networks' errors
become less correlated so it helps to train networks on different
subsets of the data (Breiman 1994). Training a net on data that
earlier nets get wrong is an effective way of focusing computational
resources on the difficult cases (Drucker, Schapire, and Simard 1993).
When fitting a network to data it
is usual to search for a single good set of weights. The correct Bayesian
method, by contrast, computes the posterior probability distribution
over weight vectors and then combines the predictions made by all
the different weight vectors in proportion to their posterior probabilities. MacKay's
methods approximate the posterior by constructing a Gaussian distribution
around each of a number of locally optimal weight vectors. Neal
(1996) describes an efficient Monte Carlo method of approximating
the full, multimodal posterior distribution. Rasmussen (1996) demonstrates
that Neal's method gives better performance than many other
neural network or statistical methods, but that it is no better
than an equivalent statistical approach called Gaussian Processes.
Many varieties of feedforward net
have been investigated. Radial basis function (RBF) networks use
hidden units whose activations are a radially symmetrical function
of the distance between the input vector and a mean vector associated
with the unit (Broomhead and Lowe 1988). The usual function is a
spherical Gaussian, but they can be generalized to have different variances
on each input dimension or to have full covariance matrices. RBF
networks can be fitted using the gradient computed by backpropagation.
Alternatively, the means and variances of the hidden units can be
set without reference to the desired outputs by fitting a mixture
of Gaussian density models to the input vectors, or by simply using
some of the training input vectors as means.
For tasks in which the data are expected
to come from a number of different but unknown regimes, it is advantageous
to use a "mixture of experts" architecture containing
a different network for each regime and a "gating" network
that decides on the probability of being in each regime (Jacobs
et al. 1991). The whole system is trained to maximize the log probability of
the correct answer under a mixture of Gaussian distributions, where
each expert computes the input-dependent mean of a Gaussian and
the gating network computes the input-dependent mixing proportion.
Each expert can specialize on a specific regime because it only
receives significant backpropagated gradients for cases where the
gating network assigns it a significant mixing proportion. The gating network
can discover the regimes because it receives backpropagated derivatives
that encourage it to assign the expert that works best for each
case. With a hierarchy of managers, this system is a soft version
of decision trees (Jordan and Jacobs 1994).
See also
-- Geoffrey Hinton
References
Bishop, C. M. (1995). Neural Networks
for Pattern Recognition. Oxford: Oxford University Press.
Breiman, L. (1994). Bagging Predictors. Technical
Report 421. Berkeley, CA: Department of Statistics, University of
California.
Broomhead, D., and D. Lowe. (1988). Multivariable
functional in-terpolation and adaptive networks. Complex Systems 2:321-355.
Churchland, P. S., and T. J. Sejnowski. (1992). The
Computational Brain. Cambridge, MA: MIT Press.
Drucker, H., R. Schapire, and P. Simard. (1993).
Improving performance in neural networks using a boosting algorithm.
In S. Hanson, J. Cowan, and C. Giles, Eds., Neural Information
Processing Systems, vol. 5. San Mateo, CA: Kaufmann, pp.
42-49.
Fahlman, S. E., and C. Lebiere. (1990). The
cascade-correlation learning architecture. In D. S. Touretzky, Ed., Neural
Information Processing Systems, vol. 2. San Mateo, CA: Kaufmann,
pp. 524-532.
Geman, S., E. Bienenstock, and R. Doursat. (1992).
Neural networks and the bias/variance dilemma. Neural
Computation 4:1-58.
Jordan, M., and R. Jacobs. (1994). Hierarchical
mixtures of experts and the EM algorithm. Neural Computation 6:181-214.
Jacobs, R., M. I. Jordan, S. J. Nowlan, and
G. E. Hinton. (1991). Adaptive mixtures of local experts. Neural
Computation 3:79-87.
Lang, K., A. Waibel, and G. E. Hinton. (1990).
A time-delay neural network architecture for isolated word recognition. Neural
Networks 3:23-43.
Le Cun, Y., B. Boser, J. S. Denker, D. Henderson,
R. E. Howard, W. Hubbard, and L. D. Jackel. (1989). Back-propagation
applied to handwritten zipcode recognition. Neural Computation 1(4):541-551.
MacKay, D. J. C. (1995). Probable networks and
plausible predictions: A review of practical Bayesian methods for
supervised neural networks. Network: Computation in Neural
Systems 6:469-505.
Minsky, M. L., and S. Papert. (1969). Perceptrons. Cambridge,
MA: MIT Press.
Neal, R. M. (1996). Bayesian Learning
for Neural Networks. New York: Springer.
Rasmussen, C. E. (1996). Evaluation of
Gaussian Processes and Other Methods for Non-linear Regression. Ph.D.
diss., University of Toronto.
Rosenblatt, F. (1962). Principles of Neurodynamics. New
York: Spartan Books.
Rumelhart, D. E., G. E. Hinton, and R. J. Williams.
(1986). Learning representations by back-propagating errors. Nature 323:533-536.
Widrow, B., and M. E. Hoff. (1960). Adaptive
switching circuits. In IRE WESCON Convention Record, part
4, pp. 96-104.
Wolpert, D. H. (1992). Stacked generalization. Neural
Networks 5:241-259.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
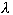 . This
can be viewed in Bayesian terms as a zero-mean Gaussian prior which
favors networks that have small weights.
. This
can be viewed in Bayesian terms as a zero-mean Gaussian prior which
favors networks that have small weights. 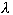 can
be chosen using a validation set but this wastes training data and
is awkward if different values of
can
be chosen using a validation set but this wastes training data and
is awkward if different values of 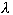 are
required for the input-to-hidden and hidden-to-output weights. MacKay (1995)
has developed Bayesian methods that estimate an appropriate
are
required for the input-to-hidden and hidden-to-output weights. MacKay (1995)
has developed Bayesian methods that estimate an appropriate
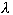 without using a validation set.
without using a validation set.