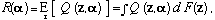
Equation 1
Statistical learning theory addresses a key question that arises when constructing predictive models from data -- how to decide whether a particular model is adequate or whether a different model would produce better predictions. Whereas classical statistics typically assumes that the form of the correct model is known and the objective is to estimate the model parameters, statistical learning theory presumes that the correct form is completely unknown and the goal is to identify the best possible model from a set of competing models. The models need not have the same mathematical form and none of them need be correct. The theory provides a sound statistical basis for assessing model adequacy under these circumstances, which are precisely the circumstances encountered in MACHINE LEARNING, PATTERN RECOGNITION, and exploratory data analysis.
Estimating the performance of competing models is the central issue in statistical learning theory. Performance is measured through the use of loss functions. The loss Q(z, α) between a data vector z and a specific model α (one with values assigned to all parameters) is a score that indicates how well α performs on z, with lower scores indicating better performance. The squared-error function for regression models, the 0/1 loss function for classification models, and the negative log likelihood for other more general statistical models are all examples of loss functions. The choice of loss function depends on the nature of the modeling problem.
From the point of view of UTILITY THEORY,α is a decision variable, z is an outcome, and Q(z, α) is the negative utility of the outcome given the decision. Hence, if the statistical properties of the data were already known, the optimum model would be the α that minimizes the expected loss R(α):
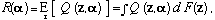
Equation 1
where F(z) is the probability measure that defines the true statistical properties of the data. R(α) is also referred to as the risk of α. In learning situations, however, F(z) is unknown and one must choose a model based on a set of observed data vectors zi, i = 1, . . . , l, that are assumed to be random samples of F(z). The average loss Remp(α, l) on the observed data is used as an empirical estimate of the expected loss, where
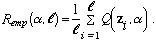
Equation 2
Remp(α, l) is also referred to as the empirical risk of α.
The fundamental question in statistical learning theory is the following: under what conditions does minimizing Remp(α, l) yield models that also minimize R(α), inasmuch as the latter is what we actually want to accomplish? This question is answered by considering the accuracy of the empirical loss estimate.
As in classical statistics, accuracy is expressed in terms of confidence regions; that is, how far can Remp(α, l) be expected to deviate from R(α), and with what probability? One of the fundamental theorems of statistical learning theory shows that the size of the confidence region is governed by the maximum difference between the two losses over all models being considered:
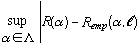
Equation 3
where Λ is a set of competing models. The maximum difference dominates because of the phenomenon of overfitting.
Overfitting occurs when the best model relative to the training data tends to perform significantly worse when applied to new data. This mathematically corresponds to a situation in which the average loss Remp(α, l) substantially underestimates the expected loss R(α). Although there is always some probability that underestimation will occur for a fixed model α, both the probability and the degree of underestimation are increased by the fact that we explicitly search for the a that minimizes Remp(α, l). This search biases the difference between R(α) and Remp(α, l) toward the maximum difference among competing models. If the maximum difference does not converge to zero as the number of data vectors l increases, then overfitting will occur with probability one.
The core results in statistical learning theory are a series of probability bounds developed by Vapnik and Chervonenkis (1971, 1981, 1991) that define small-sample confidence regions for the maximum difference between R(α) and Remp(α, l). The confidence regions differ from those obtained in classical statistics in three respects. First, they do not assume that the models are correct. Second, they are based on small-sample statistics and are not asymptotic approximations. Third, a uniform method is used to take into account the degree to which overfitting can occur for a given set of competing models. This method is based on a measurement known as the Vapnik-Chervonenkis (VC) dimension.
Conceptually speaking, the VC dimension of a set of models is the maximum number of data vectors for which overfitting is virtually guaranteed in the sense that one can always find a specific model that fits the data exactly. For example, the VC dimension of the family of linear discriminant functions with n parametric terms is n, because n linear terms can be used to discriminate exactly n points in general position for any two-class labeling of the points. This conceptual definition of VC dimension accurately reflects the formal definition in the case of 0/1 loss functions, wherein Q(z, α) = 0 if a correctly predicts z and Q(z, α) = 1 otherwise. However, the formal definition is more general in that it considers arbitrary loss functions and does not require exact fits.
In the probability bounds obtained by Vapnik and Chervonenkis, the size of the confidence region is largely determined by the ratio of the VC dimension h to the number of data vectors l. For example, if Q(z, α) is the 0/1 loss function used for classification models, then with probability at least 1 - η,
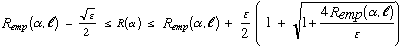
Equation 4
where
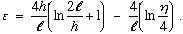
Equation 5
Note that the ratio of h over l is the dominant term in the definition of ε and, hence, in the size of the confidence region for R(α).
V. N. Vapnik (1982, 1995, 1998) has reported probability bounds for other families of loss functions that yield analogous confidence regions based on VC dimension. Bounds also exist for the special case in which the set of competing models is finite (continuous parameters typically imply an infinite number of specific models). These bounds avoid explicit calculation of VC dimension and are useful in validation-set methods. A remarkable property shared by all of the bounds is that they either make no assumptions at all or very weak assumptions about underlying probability distribution F(z). In addition, they are valid for small sample sizes and they depend only on the VC dimension of the set of competing models λ, or on its size, and on the properties of the loss function Q(z, α). All bounds are independent of the mathematical forms of the models -- the VC dimension and/or the number of specific models summarizes all relevant information. Thus, the bounds are equally applicable to both nonlinear and nonparametric models, and to combinations of dissimilar model families. This includes NEURAL NETWORKS, DECISION TREES and rules, regression trees and rules, radial basis functions, BAYESIAN NETWORKS, and so on.
When using statistical learning theory to identify the best model from a set of competing models, the models must first be ordered according to preference. The most preferable model that best explains the data is then selected. The preference order corresponds to the notion of learning bias found in machine learning. No restrictions are placed on the order other than it must be fixed prior to model selection. The ordering itself is referred to as a structure and the process of selecting models is called structural risk minimization.
Structural risk minimization has two components: one is to determine a cutoff point in the preference ordering, the other is to select the best model from among those that occur before the cutoff. As the cutoff point is advanced through the ordering, both the subset of models that appear before the cutoff and the VC dimension of this subset steadily increase. With more models to choose from, the minimum average loss Remp(α, l) for all models α before the cutoff tends to decrease. However, the size of the confidence region for R(α) tends to increase because the size is governed by the VC dimension. The cutoff point is selected by minimizing the upper bound on the confidence region for R(α), with the corresponding α chosen as the most suitable model given the available data. For example, for classification problems one would choose the cutoff and the associated model α so as to minimize the right hand side of the inequality presented above for a desired setting of the confidence parameter η.
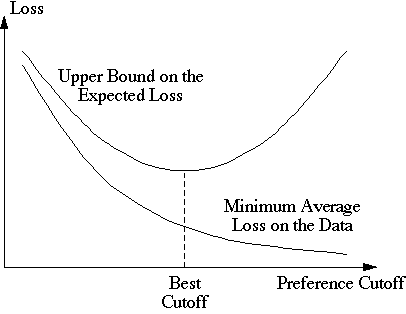
Figure 1 For each cutoff point in the model preference ordering, one selects the model that minimizes the average loss on the data from among those that occur before the cutoff. The most suitable model for the data is then the one with the smallest upper bound on the expected loss.
The overall approach is illustrated by the graph in figure 1. The process balances the ability to find increasingly better fits to the data against the danger of overfitting and thereby selecting a poor model. The preference order provides the necessary structure in which to compare competing models. Judicious choice of the model order enables one to avoid overfitting even in high-dimensional spaces. For example, Vapnik and others (Cortes and Vapnik 1995; Vapnik 1995, 1998) order models within parametric families according to the magnitudes of the parameters. Each preference cutoff then limits the parameter magnitudes, which in turn limits the VC dimension of the corresponding subset of models. Reliable models can thus be obtained using structural risk minimization even when the number of data samples is orders of magnitude less than the number of parameters.
Cortes, C., and V. N. Vapnik. (1995). Support vector machines. Machine Learning 20:273-297.
Vapnik, V. N., and A. J. Chervonenkis. (1971). On the uniform convergence of relative frequencies of events to their probabilities. Theory of Probability and Its Applications 16:264-280. Original work published 1968 as Doklady Akademii Nauk USSR 181(4).
Vapnik, V. N., and A. J. Chervonenkis. (1981). Necessary and sufficient conditions for the uniform convergence of means to their expectations. Theory of Probability and Its Applications 26:532-553.
Vapnik, V. N., and A. J. Chervonenkis. (1991). The necessary and sufficient conditions for consistency of the method of empirical risk minimization. Pattern Recognition and Image Analysis 1:284-305. Original work published as Yearbook of the Academy of Sciences of the USSR on Recognition, Classification, and Forecasting 2 (1989).
Vapnik, V. N. (1982). Estimation of Dependencies Based on Empirical Data. New York: Springer.
Vapnik, V. N. (1995). The Nature of Statistical Learning Theory. New York: Springer.
Vapnik, V. N. (1998). Statistical Learning Theory. New York: Wiley.
Biggs, N., and M. H. G. Anthony. (1992). Computational Learning Theory: An Introduction. Cambridge Tracts in Theoretical Computer Science, No. 30. London: Cambridge University Press.
Devroye, L., L. Gyorfi, and G. Lugosi. (1996). A Probabilistic Theory of Pattern Recognition. New York: Springer.
Dudley, R. M. (1984). A course on empirical processes. In R. M. Dudley, H. Kunita, and F. Ledrappier, Eds., École d'Été de Probabilités de Sainte-Flour XII - 1982. Lecture Notes in Mathematics, vol. 1097. New York: Springer, pp. 1-142.
Kearns, M. J., and U. V. Vazirani. (1994). An Introduction to Computational Learning Theory. Cambridge, MA: MIT Press.
Parrondo, J. M. R., and C. Van den Broeck. (1993). Vapnik-Chervonenkis bounds for generalization. Journal of Physics A 26:2211-2223.
Pollard, D. (1984). Convergence of Stochastic Processes. New York: Springer.
Pollard, D. (1990). Empirical Processes: Theory and Applications. NSF-CBMS Regional Conference Series in Probability and Statistics, vol. 2. Hayward, CA: Institute of Mathematical Statistics.
Shawe-Taylor, J. S., A. Macintyre, and M. Jerrum, Eds. (1998). Special Issue on the Vapnik-Chervonenkis Dimension. Discrete Applied Mathematics 86(1).
Vidyasagar, M. (1997). A Theory of Learning and Generalization: With Applications to Neural Networks and Control Systems (Communications and Control Engineering). New York: Springer.