Over the past few decades, NEURAL NETWORKS have provided the dominant framework for understanding how the brain implements the computations necessary for its survival. At the heart of these networks are very dynamic and complex processing nodes, individual neurons. A typical NEURON in the CEREBRAL CORTEX receives input from a few thousand fellow neurons and, in turn, passes on messages to a few thousand other neurons. One hundred thousand such cells are packed into a cubic millimeter of cortical tissue, which amounts to 4 kilometers of axonal wiring, 500 meters of dendrites, and close to one billion synapses (Braitenberg and Schüz 1991).
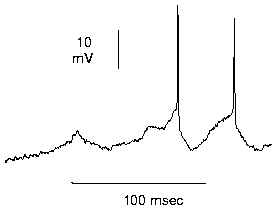
Synapses, the specialized connections between two neurons, come in two basic flavors, excitatory and inhibitory. An excitatory synapse will reduce the electrical potential across the membrane of its target cell (that is, it will depolarize the cell), while an inhibitory synapse will hyperpolarize the cell. If the membrane potential at the cell body exceeds a particular threshold value, the neuron generates a short, millisecond-long pulse, called an "action potential" or "spike" (figure 1). Otherwise, it remains silent. The amount of synaptic input determines how fast the cell generates spikes, and these are in turn conveyed to the next target cells through the output axon. Information processing in an average human cortex then relies on the proper interconnection of about 4 × 1010 such neurons in a network of stupendous size.

Figure 1 Action potentials recorded in a single neuron in the visual cortex, shown as a plot of membrane potential against time. (a) A visual stimulus causes a sustained barrage of synaptic input, which triggers three cycles of depolarization. The first cycle does not reach the threshold for generating a spike, but the second and third do. Each spike lasts for about 1 msec. (Data provided by B. Ahmed, N. Berman, and K. Martin.)
In 1943, MCCULLOCH and PITTS showed that this view is at least plausible. They described each synapse by a single scalar weight, ranging from positive to negative depending on whether the synapse was excitatory or inhibitory. The contributions from all synapses, multiplied by their synaptic weights, add linearly at the cell body. If this sum exceeds a threshold, a spike is generated. McCulloch and Pitts argued that, with the addition of memory, a sufficiently large number of these logical "neurons," wired together in an appropriate manner, can compute anything that can be computed on any digital computer.
LEARNING entered this picture in the form of HEBB's (1949) rule, postulating that the synapse between neuron A and neuron B increases its "weight" if activity in A occurs at the same time as activity in B. Half a century later, we have solid evidence that such changes do take place in a well-studied phenomenon termed LONG- TERM POTENTIATION (LTP). Here, the synaptic weight increases for days or even weeks. It can be induced by simultaneous activity at the pre- and postsynaptic termini, in agreement with Hebb's rule (Nicoll and Malenka 1995). Of more recent vintage is the discovery of a complementary process, a decrease in synaptic weight called "long-term depression" (Stevens 1996).
Over the last few years, it has become abundantly clear that dendrites do much more than simply convey synaptic inputs to the cell body for linear summation. Dendrites have traditionally been treated as passive cables, surrounded by a membrane that can be modeled by a conductance in parallel with a capacitance (Segev, Rinzel, and Shepherd 1995). When synaptic input is applied, such an arrangement acts as a low-pass filter, removing the high frequencies but performing no other significant information processing. Dendrites with such a passive membrane would not really disturb our view of neurons as linear threshold units.
As long ago as the 1950s, Hodgkin and Huxley (1952) showed how the transient changes in such active voltage-dependent membrane conductances generate and shape the action potential. But it was assumed that they are limited to the axon and the adjacent cell body. We now know that many dendrites of pyramidal cells are endowed with a relatively homogeneous distribution of sodium conductances as well as a diversity of calcium membrane conductances (Johnston et al. 1996).
What is the function of these active conductances? One likely explanation (supported by computer models) is that calcium and potassium membrane conductances in the distant dendrites can selectively linearize and amplify this input. Voltage-dependent conductances can also subserve a specific nonlinear operation, multiplication, one of the most common operations carried out in the nervous system (Koch and Poggio 1992). If the dendritic tree contains sodium or calcium conductances, or if the synapses use a particular type of receptor (the so-called NMDA receptor), the inputs can interact synergistically, with the strongest response occurring when inputs from different neurons are located close to each other on a patch of dendritic membrane. Simulations (Mel 1994) show that the firing rate of such a neuron is proportional to the product, rather than the sum, of its inputs.
Ramòn y CAJAL postulated the law of "dynamic polarization," stipulating that dendrites and cell bodies are the receptive areas for the synaptic input, and that the resulting output pulses are transmitted unidirectionally along the axon to its targets. From work on brain slices, however, it seems that this is by no means the whole story. Single action potentials can propagate not only forward from their initiation site along the axon, but also backward into the dendritic tree, a phenomenon known as antidromic spike invasion (Stuart and Sakmann 1994). It remains unclear whether dendrites themselves can initiate action potentials. If spikes can be generated locally under physiological conditions, they could implement powerful logical operations far away from the cell body (Softky 1994).
What of the role of time in neuronal processing? There are two main aspects to this issue: (1) the relationship between the timing of an event in the external world and the timing of the representation of that event at the single-neuron level; (2) the accuracy and importance of the relative timing of spikes between two or more neurons.
Regarding the first aspect, some animals can discriminate intervals of the order of a microsecond (for instance, to localize sounds), implying that the timing of sensory stimuli must be represented with similar precision in the brain, and is probably based on the average timing of spikes in a population of cells. It is also possible to measure the precision with which individual cells track the timing of external events. For instance, certain cells in the monkey VISUAL CORTEX are preferentially stimulated by moving stimuli, and these cells can modulate their firing rate with a precision of less than 10 msec (Bair and Koch 1996).
The second aspect of the timing issue is the extent to which the exact temporal arrangements of spikes -- both within a single neuron and across several neurons -- matters for information processing. It is usually assumed that, to cope with the apparent lack of reliability of single cells, the brain makes use of a "firing rate" code. Only the average number of spikes within some suitable time window, say a fraction of a second, matters. The detailed pattern of spikes (figure 2) is thought by many to be largely irrelevant, a hypothesis supported by the existence of a quantitative relationship between the firing rates of single cortical neurons and psychophysical judgments made by monkeys. That is, the behavior of a monkey in a visual discrimination task can be statistically predicted by counting spikes in a single neuron in the visual cortex (Newsome, Britten, and Movshon 1989). Robustness of this encoding is further ensured by averaging the response over a large number of similar cells (a process known as population coding).

Figure 2 Variability in neuronal responses (each line in the trace corresponds to a spike of the type shown in figure 1). If the same stimulus is presented twice in succession, it induces the same average firing rate on both trials (about 50 Hz), although the exact timing of individual spikes shows random variation. (Data provided by W. Newsome and K. Britten.)
Recent years have witnessed a resurgence in information-theoretic approaches to the nervous system (Rieke et al. 1996). We know that individual neurons, such as motion-selective cells in the fly or single auditory inputs in the bullfrog, can encode between 1 and 3 bits of sensory information per output spike, amounting to rates of up to 300 bits per second. This information is encoded using changes in the instantaneous interspike interval between a handful of spikes. Such a temporal encoding mechanism is within 10 to 40 percent of the theoretical maximum allowed by the spike train variability. This implies that individual spikes can carry significant amounts of information, at odds with the idea that neurons are unreliable and can only signal in the aggregate. At these rates, the optic nerve would convey between one and ten million bits per second. (This compares to a ten-speed CD-ROM drive, which transfers information at 1.5 million bits per second.)
Timing precision of spiking across populations of simultaneously firing neurons is believed to be a key element in neuronal strategies for encoding perceptual information in the sensory pathways (Abeles 1990; Singer and Gray 1995). Yet if information is indeed embodied in a temporal code, how, if at all, is it decoded by the target neurons? Do neurons act as coincidence detectors, able to detect the arrival time of incoming spikes at a millisecond or better resolution? Or do they integrate more than a hundred or so relatively small inputs over many tens of milliseconds until the threshold for spike initiation is reached (Softky 1995; see figure 1)?
Current thinking about computation has the brain as a hybrid computer. Individual nerve cells convert the incoming streams of binary pulses into analog, spatially distributed variables: the postsynaptic membrane potential and calcium distribution throughout the dendritic tree. This transformation involves highly dynamic synapses that adapt to their input. Information is then processed in the analog domain, using a number of linear and nonlinear operations (multiplication, saturation, amplification, thresholding) implemented in the dendritic cable structure and augmented by voltage-dependent membrane and synaptic conductances. The result is converted into asynchronous binary pulses and conveyed to the following neurons. The functional resolution of these pulses is in the millisecond range, with temporal synchrony across neurons likely to contribute to coding. Reliability could be achieved by pooling the responses of a small number (20-200) of neurons.
And what of MEMORY? It is everywhere (but cannot be randomly accessed). It resides in the concentration of free calcium in dendrites and cell body; in the presynaptic terminal; in the density and exact voltage dependency of the various ionic conductances; in the density and configuration of specific proteins in the postsynaptic terminals; and, ultimately, in the gene in the cell's nucleus for lifetime memories.
Abeles, M. (1990). Corticonics: Neural Circuits of the Cerebral Cortex. Cambridge University Press.
Bair, W. and C. Koch. (1996). Temporal precision of spike trains in extrastriate cortex of the behaving monkey. Neural Computation 8:1185-1202.
Braitenberg, V., and A. Schüz. (1991). Anatomy of the Cortex. Berlin: Springer.
Hebb, D. O. (1949). The Organization of Behavior: A Neuropsychological Theory. New York: Wiley.
Hodgkin, A. L., and A. F. Huxley. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500-544.
Johnston, D., J. Magee, C. Colbert, and B. Christie. (1996). Active properties of neuronal dendrites. Annu. Rev. Neurosci 19:165-186.
Koch, C., and T. Poggio. (1992). Multiplying with synapses and neurons. In T. McKenna, J. Davis, and S. F. Zornetzer, Eds., Single Neuron Computation. Boston: Academic Press, pp. 315-345.
McCulloch, W., and W. Pitts. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics 5:115-133.
Mel, B. W. (1994). Information processing in dendritic trees. Neural Computation 6:1031-1085.
Newsome, W. T., K. H. Britten, and J. A. Movshon (1989). Nature 341:52-54.
Nicoll, R. A., and R. C. Malenka. (1995). Contrasting properties of two forms of longterm potentiation in the hippocampus. Nature 377:115-118.
Rieke, F., D. Warland, R. R. D. van Steveninck, and W. Bialek. (1996). Spikes: Exploring the Neural Code. Cambridge, MA: MIT Press.
Segev, I., J. Rinzel, and G. Shepherd. (1995). The Theoretical Foundation of Dendritic Function: Selected Papers of Wilfrid Rall with Commentaries. Cambridge, MA: MIT Press.
Singer, W., and C. M. Gray. (1995). Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci 18:555-586.
Softky, W. R. (1994). Sub-millisecond coincidence detection in active dendritic trees. Neuroscience 58:15-41.
Softky, W. R. (1995). Simple codes versus efficient codes. Curr. Opin. Neurobiol 5:239-247.
Stevens, C. F. (1996). Strengths and weaknesses in memory. Nature 381:471-472.
Stuart, G. J., and B. Sakmann. (1994). Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature 367:69-72.
Arbib, M., Ed. (1995). The Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press.
Hopfield, J. J. (1995). Pattern-recognition computation using action potential timing for stimulus representation. Nature 376:33-36
Koch, C. (1998) Biophysics of Computation: Information Processing in Single Neurons. New York: Oxford University Press.
Koch, C., and I. Segev, Eds. (1998). Methods in Neuronal Modeling: From Ions to Networks. Second edition. Cambridge, MA: MIT Press.
Shepherd, G., Ed. (1998). The Synaptic Organization of the Brain. Fourth edition. New York: Oxford University Press.
Supplementary information can be found at http://www.klab. caltech.edu