Metareasoning is reasoning about reasoning -- in its broadest sense, any computational process concerned with the operation of some other computational process within the same entity. The term relies on a conceptual distinction between object-level deliberation about external entities, for example, considering the merits of various opening moves one might make in a game of chess, and metalevel deliberation about internal entities (computations, beliefs, and so on), for example, deciding that it is not worth spending much time deliberating about which opening move to make. Genesereth and Nilsson (1987) provide formal definitions along these lines. Smith (1986) makes a further distinction between INTROSPECTION about purely internal entities and reflection relating internal and external entities. In this view, a proposition such as "If I open the window I will know if the birds are singing" is reflective, because it relates a physical action to a future state of knowledge.
The capacity for metareasoning serves several purposes in an intelligent agent. First, it allows the agent to control its object-level deliberations -- to decide which ones to undertake and when to stop deliberating and act. This is essential, given the pervasive problem of COMPUTATIONAL COMPLEXITY in decision making, and the consequent need for BOUNDED RATIONALITY. In GAME-PLAYING SYSTEMS, for example, the alpha-beta ALGORITHM makes a simple metalevel decision to avoid certain lines of deliberation about future moves, taking advantage of a metalevel theorem to the effect that these lines cannot affect the ultimate object-level decision. Second, metareasoning allows the agent to generate computational and physical behaviors, such as planning to obtain information, that require introspective or reflective reasoning. Third, it allows the agent to recover from errors or impasses in its object-level deliberations.
Most early work on metareasoning focused on designing an INTELLIGENT AGENT ARCHITECTURE (see also COGNITIVE ARCHITECTURE) that could support introspection and reflection. The use of metareasoning to control deduction seems to have been proposed first by Hayes (1973), although the first implementation was in the TEIRESIAS system (Davis 1980), which used metarules to control deliberation within a rule-based expert system. The Metalevel Representation System, or MRS, (Genesereth and Smith 1981) used LOGIC PROGRAMMING for both object and metalevel inference and provided a very flexible interface between the two. Because MRS allowed reasoning about which procedure to use for each object-level inference, and about which representation to use for each object-level fact, it enabled many different representations and reasoning methods to operate together seamlessly. By far the most ambitious metalevel architecture is Soar (Laird, Newell, and Rosenbloom 1987), whose fundamental mode of computation is based on PROBLEM SOLVING. Whenever Soar does not have an unambiguous rule telling it which problem-solving step to take next, it invokes universal subgoaling to set up a metalevel problem space that will resolve the issue. As might be imagined from these examples, designers of such systems must take care to avoid an infinite regress of metameta . . . reasoning.
Does metareasoning differ from "ordinary" reasoning? In all metalevel architectures, the metalevel is given direct access to object-level data structures. Thus metareasoning (at least in computers) can assume a completely and perfectly observable object-level state -- which is seldom the case with ordinary reasoning about the external world. Furthermore, it is possible to represent fully and exactly the nature of the available object-level computations. Thus it is possible for the metalevel to simulate completely the object-level computations under consideration (as is done in Soar). This would seem counterproductive, however, as a way of selecting among object-level computations because simulating a computation (and hence knowing its outcome) is just a very slow way of doing the computation itself -- knowledge of the outcome of a computation is the outcome. For this reason, Soar always compiles the results of subgoaling into a new rule, thereby avoiding deliberation in similar cases in future. Compilation of metareasoning into more efficient forms is perhaps the principal way an agent's computational performance can improve over time.
In the research outlined thus far, the metareasoning consisted mostly of applying simple "IF-THEN" rules encoding the system designer's computational EXPERTISE; no standard of rationality for metareasoning was provided. The concept of rational metareasoning (Horvitz 1989; Russell and Wefald 1989) had its roots in early work by I. J. Good (1971) on "Type II rationality" and in information value theory (Howard 1966), which places a value on acquiring a piece of information based on the expected improvement in decision quality that results from its acquisition. A COMPUTATION can be viewed as the process of making explicit some information that was previously implicit, and therefore value can be placed on computations in the same way. That is, a computation can be viewed as an action whose benefit is that it may result in better external decisions, and whose cost is the delay it incurs. Thus, given a model of the effects of computations and information about object-level utility, the metalevel can infer the value of computations. It can decide which computations to do and when computation should give way to action.

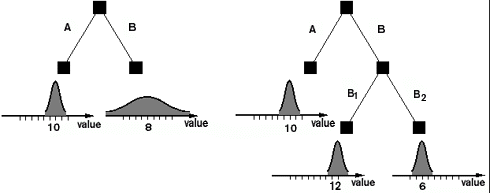
Figure 1. The consequence of computation: Lookahead reveals that B may in fact be better than A.
The simplest applications of rational metareasoning arise in the context of anytime algorithms (Horvitz 1987; Dean and Boddy 1988), that is, algorithms that can be interrupted at any time and whose output quality improves continuously with time. Each such algorithm has an associated performance profile describing its output quality as a function of time. The availability of the profile makes the metalevel decision problem -- which algorithm to run and when to terminate -- fairly trivial. The use of anytime algorithms devised for a wide variety of computational tasks has resulted in a widely applicable methodology for building complex, real-time decision-making systems (Zilberstein and Russell 1996).
A finer-grained approach to metareasoning can be obtained by evaluating individual computation steps within an algorithm. Consider the decision-making situation shown in figure 1a. An agent has two possible actions, A and B. Based on a quick assessment, the outcome of A appears to be worth 10 with a standard deviation of 1, whereas the outcome of B seems to be worth 8 with a standard deviation of 4. The agent can choose A immediately, or it can refine its estimates by looking further into the future. For example (figure 1b), it can consider the actions B1 and B2, with the outcomes shown. At this point, action B (followed by B1) seems to lead to a state with value 12; thus the lookahead computation has changed the agent's decision, with an apparent benefit of 2. Obviously, this is a post hoc analysis, but, as shown by Russell and Wefald (1991), an expected value of computation can be computed efficiently -- prior to performing the lookahead. In figure 1a, this value is 0.3 for lookahead from A and 0.82 for lookahead from B. If the initial estimated outcome of A were 12, however, these values would drop to 0.002 and 0.06, respectively. Hence, as one would expect, the value of computation depends strongly on whether a clear choice of action has already emerged. If, however, the initial estimates for A and B were both 10, with standard deviations of 0.1, then the value of computation becomes 0.03. Computation is worthless when it does not matter which action one eventually chooses.
Rational metareasoning can be applied to control deliberations in a wide variety of object-level algorithms including HEURISTIC SEARCH and game playing (Russell and Wefald 1991), LOGICAL REASONING SYSTEMS (Smith 1989), and MACHINE LEARNING (Rivest and Sloan 1988). An important insight to emerge from this work is that a metareasoning capability can, in principle, be domain independent (Russell and Wefald 1991; Ginsberg and Geddis 1991) because the necessary domain-specific information (such as the utility function) can be extracted from the object level. One can therefore view successful computational behavior as emerging not from carefully crafted, domain-specific algorithms but from the interaction of a general capacity for rational metareasoning with object-level domain knowledge. More efficient, domain-specific computational behaviors might then result from processes of compilation and metalevel REINFORCEMENT LEARNING.
Davis, R. (1980). Meta-rules: Reasoning about control. Artificial Intelligence 15(3):179-222.
Dean, T., and M. Boddy. (1988). An analysis of time-dependent planning. In Proceedings of the Seventh National Conference on Artificial Intelligence (AAAI-88). St. Paul, MN: Kaufmann, pp. 49-54.
Genesereth, M. R., and D. Smith. (1981). Meta-level architecture. Memo HPP-81-6. Computer Science Department, Stanford University.
Genesereth, M. R., and N. J. Nilsson. (1987). Logical Foundations of Artificial Intelligence. San Mateo, CA: Kaufmann.
Ginsberg, M. L., and D. F. Geddis. (1991). Is there any need for domain-dependent control information? In Proceedings of the Ninth National Conference on Artificial Intelligence, vol. 1. (AAAI-91). Anaheim, California: AAAI Press, pp. 452-457.
Good, I. J. (1971). Twenty-seven principles of rationality. In V. P. Godambe and D. A. Sprott, Eds., Foundations of Statistical Inference. Toronto: Holt, Rinehart and Winston, pp. 108-141.
Hayes, P. J. (1973). Computation and deduction. In Proceedings of the Second Symposium on Mathematical Foundations of Computer Science Czechoslovakia. Czechoslovakian Academy of Science.
Horvitz, E. J. (1987). Problem-solving design: Reasoning about computational value, trade-offs, and resources. In Proceedings of the Second Annual NASA Research Forum. Moffett Field, CA: NASA Ames Research Center, pp. 26-43.
Horvitz, E. J. (1989). Reasoning about beliefs and actions under computational resource constraints. In L. N. Kanal, T. S. Levitt, and J. F. Lemmer, Eds., Uncertainty in Artificial Intelligence, vol. 3. Amsterdam: Elsevier, pp. 301-324.
Howard, R. A. (1966). Information value theory. IEEE Transactions on Systems Science and Cybernetics SSC-2:22-26.
Laird, J. E., A. Newell, and P. S. Rosenbloom. (1987). SOAR: An architecture for general intelligence. Artificial Intelligence 33(1):1-64.
Rivest, R. L., and R. Sloan. (1988). A new model for inductive inference. In M. Vardi, Ed., Proceedings of the Second Conference on Theoretical Aspects of Reasoning about Knowledge. San Mateo, CA: Kaufmann, pp. 13-27.
Russell, S. J., and E. H. Wefald. (1989). On optimal game-tree search using rational metareasoning. Proceedings of the Eleventh International Joint Conference on Artificial Intelligence (IJCAI-89). Detroit: Kaufmann, pp. 334-340.
Russell, S. J., and E. H. Wefald. (1991). Do the Right Thing: Studies in Limited Rationality. Cambridge, MA: MIT Press.
Smith, B. C. (1986). Varieties of self-reference. In J. Halpern, Ed., Theoretical Aspects of Reasoning about Knowledge. San Mateo, CA: Kaufmann.
Smith, D. E. (1989). Controlling backward inference. Artificial Intelligence 39(2):145-208.
Zilberstein, S., and S. Russell. (1996). Optimal composition of real-time systems. Artificial Intelligence 83.