Utility Theory
The branch
of decision theory concerned with measurement and representation
of preferences is called utility theory. Utility theorists focus
on accounts of preferences in RATIONAL DECISION MAKING, where
an individual's preferences cohere with associated beliefs
and actions. Utility refers to the scale on which preference
is measured.
Identification of preference measurement
as an issue is usually credited to Daniel Bernoulli (1954/1738),
who exhibited a prospect (probability distribution over outcomes)
that had infinite expected monetary value, but apparently not infinite
utility. Bernoulli resolved the "St. Petersburg paradox" by
suggesting that utility be logarithmic in monetary amounts, which in
this case would yield a finite expected utility.
That utility could apply to all sorts
of outcomes, not merely monetary rewards, was first argued forcefully
by Jeremy Bentham (1823/1789), who proposed a system for
tabulating "pleasures" and "pains" (positive
and negative utility factors), which he called the "hedonic
calculus" (regrettably, as critics henceforth have confounded
the idea of universal preference measurement with hedonism). Bentham
further argued that these values could be aggregated across society
("greatest good for the greatest number"), which
became the core of an ethical doctrine known as utilitarianism (Albee 1901).
Although modern economists are quite
reluctant to aggregate preferences across individuals, the concept
of individual utility plays a foundational role in the standard
neoclassical theory. Recognition of this role was the result of
the so-called marginal utility revolution of the 1870s, in which
Carl Menger, W. Stanley Jevons, Francis Ysidro Edgeworth, Léon Walras, and
other leading "marginalists" demonstrated that
values/prices could be founded on utility.
The standard theory of utility starts with a preference order,
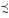 , typically taken to be a complete preorder over
the outcome space, J. y
, typically taken to be a complete preorder over
the outcome space, J. y 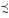 x means that
x is (weakly) preferred to y, and if in addition
¬ (x
x means that
x is (weakly) preferred to y, and if in addition
¬ (x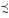 y), x is strictly
preferred. Granting certain topological assumptions, the preference
order can be represented by a real-valued utility function,
y), x is strictly
preferred. Granting certain topological assumptions, the preference
order can be represented by a real-valued utility function, 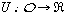 , in
the sense that U(y) ≤ U(x) if
and only if y
, in
the sense that U(y) ≤ U(x) if
and only if y 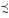 x. If
U represents
x. If
U represents 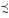 , then so does j
° U, for any monotone function j on the real
numbers. Thus, utility is an ordinal scale (Krantz et al. 1971).
, then so does j
° U, for any monotone function j on the real
numbers. Thus, utility is an ordinal scale (Krantz et al. 1971).
Under UNCERTAINTY,
the relevant preference comparison is over prospects rather than
outcomes. One can extend the utility-function representation to
prospects by taking expectations with respect to the utility for constituent
outcomes. Write [F,p; F"] to denote
the prospect formed by combining prospects F and F" with
probabilities p and 1 - p, respectively.
If F(ω) denotes the probability of outcome ω in prospect F, then
[F, p; F'](ω) ≡
p F(ω) + (1 - p) F'(ω).
The independence axiom of
utility theory states that if
F" 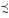 F"", then
for any prospect F and probability p,
F"", then
for any prospect F and probability p,
[F', p; F]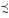 [F'', p; F]
[F'', p; F]
In other words, preference
is decomposable according to the prospect's exclusive possibilities.
Given the properties of an order
relation, the independence axiom, and an innocuous continuity condition,
preference for a prospect can be reduced to the expected value
of the outcomes in its probability distribution. The expected utility Û of
a prospect F is defined by
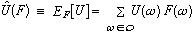
For the continuous case, replace the sum by an appropriate integral
and interpret F as a probability density function. Because
expectation is generally not invariant with respect to monotone
transformations, the measure of utility for the uncertain case must be
cardinal rather than ordinal. As with preferences over outcomes, the
utility function representation is not unique. If U is a
utility function representation of 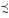 and
and 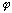 a positive linear (affine)
function on the reals, then
a positive linear (affine)
function on the reals, then 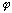 ° u also represents
° u also represents 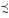 .
.
Frank Plumpton Ramsey (1964/1926)
was the first to derive expected utility from axioms on preferences
and belief. The concept achieved prominence in the 1940s, when John VON NEUMANN and Oskar Morgenstern presented an axiomatization
in their seminal volume on GAME THEORY (von Neumann
and Morgenstern 1953). (Indeed, many still refer to "vN-M
utility.") Savage (1972) presented what is now considered
the definitive mathematical argument for expected utility from the
Bayesian perspective.
Although it stands as the cornerstone
of accepted decision theory, the doctrine is not without its critics. Allais
(1953) presented a compelling early example in which most individuals
would make choices violating the expectation principle. Some have
accounted for this by expanding the outcome description to include
determinants of regret (see Bell 1982), whereas others (particularly
researchers in behavioral DECISION MAKING)
have constructed alternate preference theories (Kahneman and TVERSKY's
1979 prospect theory) to account for this as well as other phenomena.
Among those tracing the observed deviations to the premises, the independence
axiom has been the greatest source of controversy. Although the
dispute centers primarily around its descriptive validity, some
also question its normative status. See Machina (1987, 1989) for
a review of alternate approaches and discussion of descriptive and
normative issues.
Behavioral models typically posit
more about preferences than that they obey the expected utility
axioms. One of the most important qualitative properties is risk
aversion, the tendency to prefer the expected value of a prospect
to the prospect itself. For scalar outcomes, the risk aversion function
(Pratt 1964),
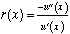
is the standard measure
of this tendency. Properties of the risk aversion measure (e.g.,
is constant, proportional, or decreasing) correspond to analytical
forms for utility functions (Keeney and Raiffa 1976), or stochastic
dominance tests for decision making (Fishburn and Vickson 1978).
When outcomes are multiattribute
(nonscalar), the outcome space is typically too large to consider
specifying preferences without imposing some structure on the utility
function. Independence concepts for preferences (Bacchus and Grove 1996; Gorman
1968; Keeney and Raiffa 1976) -- analogous to those for probability -- define
conditions under which preferences for some attributes are invariant
with respect to others. Such conditions lead to separability of
the multiattribute utility function into a combination of subutility
functions of lower dimensionality.
Modeling risk aversion, attribute
independence, and other utility properties is part of the domain
of decision analysis (Raiffa 1968; Watson and Buede 1987), the methodology
of applied decision theory. Decision analysts typically construct
preference models by asking decision makers to make hypothetical choices
(presumably easier than the original decision), and combining these
with analytical assumptions to constrain the form of a utility function.
Designers of artificial agents must
also specify preferences for their artifacts. Until relatively recently,
Artificial Intelligence PLANNING techniques
have generally been limited to goal predicates, binary indicators
of an outcome state's acceptability. Recently, however,
decision-theoretic methods have become increasingly popular, and many
developers encode utility functions in their systems. Some researchers
have attempted to combine concepts from utility theory and KNOWLEDGE REPRESENTATION to develop flexible preference models suitable
for artificial agents (Bacchus and Grove 1996; Haddawy and Hanks
1992; Wellman and Doyle 1991), but this work is still at an early
stage of development.
See also
Additional links
-- Michael P. Wellman
References
Albee, E. (1901). A History of English
Utilitarianism. London: Macmillan.
Allais, M. (1953). Le comportment de l'homme
rationnel devant la risque: Critique des postulats et axiomes de
l'école Americaine. Econometrica 21:503-546.
Bacchus, F., and A. J. Grove. (1996). Utility
independence in a qualitative decision theory. In (KR-96),
Proceedings of the Fifth International Conference on the Principles
of Knowledge Representation and Reasoning. Los Altos, CA:
Morgan Kaufmann, pp. 542-552.
Bell, D. E. (1982). Regret in decision making
under uncertainty. Operations Research 30:961-981.
Bentham, J. (1823/1789). Principles
of Morals and Legislation. Oxford: Oxford University Press.
Original work published in 1789.
Bernoulli, D. (1954). Exposition of a new theory
of the measurement of risk. Econometrica 22:123-136.
(Translation of Specimen theoriae novae de mensura sortis 1738.)
Debreu, G. (1959). Theory of Value: An
Axiomatic Analysis of Economic Equilibrium. New York: Wiley.
Fishburn, P. C., and R. G. Vickson. (1978).
Theoretical foundations of stochastic dominance. In G. A. Whitmore
and M. C. Findlay, Eds., Stochastic Dominance: An Approach
to Decision Making Under Risk. Lexington, MA: D. C. Heath
and Company.
Gorman, W. M. (1968). The structure of utility
functions. Review of Economic Studies 35:367-390.
Haddawy, P., and S. Hanks. (1992). Representations
for decision-theoretic planning: Utility functions for deadline
goals. In (KR-92) Proceedings of the Third International Conference
on the Principles of Knowledge Representation and Reasoning. San
Mateo, CA: Morgan Kaufmann, pp. 71-82.
Kahneman, D., and A. Tversky. (1979). Prospect
theory: An analysis of decision under risk. Econometrica 47:263-291.
Keeney, R. L., and H. Raiffa. (1976). Decisions
with Multiple Objectives: Preferences and Value Tradeoffs. New
York: Wiley.
Krantz, D. H., R. D. Luce, P. Suppes, and A.
Tversky. (1971). Foundations of Measurement. New York:
Academic Press.
Machina, M. J. (1987). Choice under uncertainty:
Problems solved and unsolved. Journal of Economic Perspectives 1:121-154.
Machina, M. J. (1989). Dynamic consistency and
non-expected utility models of choice under uncertainty. Journal
of Economic Literature 27(4):1622-1668.
Pratt, J. W. (1964). Risk aversion in the small
and in the large. Econometrica 32:122-136.
Raiffa, H. (1968). Decision Analysis:
Introductory Lectures on Choices Under Uncertainty. Reading,
MA: Addison-Wesley.
Ramsey, F. P. (1964/1926). Truth and probability.
In H. E. Kyburg, Jr. and H. E. Smokler, Eds., Studies in Subjective
Probability. New York: Wiley.
Savage, L. J. (1972). The Foundations
of Statistics. 2nd ed. New York: Dover Publications.
von Neumann, J., and O. Morgenstern. (1953). Theory
of Games and Economic Behavior. 3rd ed. Princeton, NJ: Princeton
University Press.
Watson, S. R., and D. M. Buede. (1987). Decision
Synthesis: The Principles and Practice of Decision Analysis. Cambridge:
Cambridge University Press.
Wellman, M. P., and J. Doyle. (1991). Preferential
semantics for goals. In Proceedings of the National Conference
on Artificial
Intelligence. Anaheim, CA: AAAI, pp. 698-703.
 Copyright © 1999 Massachusetts Institute of Technology
Copyright © 1999 Massachusetts Institute of Technology
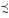 , typically taken to be a complete preorder over
the outcome space, J. y
, typically taken to be a complete preorder over
the outcome space, J. y 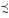 x means that
x is (weakly) preferred to y, and if in addition
¬ (x
x means that
x is (weakly) preferred to y, and if in addition
¬ (x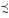 y), x is strictly
preferred. Granting certain topological assumptions, the preference
order can be represented by a real-valued utility function,
y), x is strictly
preferred. Granting certain topological assumptions, the preference
order can be represented by a real-valued utility function, 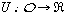 , in
the sense that U(y) ≤ U(x) if
and only if y
, in
the sense that U(y) ≤ U(x) if
and only if y 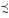 x. If
U represents
x. If
U represents 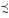 , then so does j
° U, for any monotone function j on the real
numbers. Thus, utility is an ordinal scale (Krantz et al. 1971).
, then so does j
° U, for any monotone function j on the real
numbers. Thus, utility is an ordinal scale (Krantz et al. 1971).
 a positive linear (affine)
function on the reals, then
a positive linear (affine)
function on the reals, then